程序分析之Loops in Flow Graphs

Posted on

此文为编译原理(龙书)9.6章， 补充南大重续分析第6节之后。

1. 支配结点

定义

支配结点

Dominators, 即支配结点， 如果从一段程序的entry point 到结点n的所有路径， 都经过结点m，那么我们就可以说m支配n，记为 m dom n

支配结点性质：

  • reflexive: a dom a （每个结点支配本身，不过为了区分的本身的支配结点也可以叫strict dom）
  • transitive: a dom b and b dom c => a dom c (具有传递性)
  • antisymmetric: a dom b and b dom a => a==b

直接支配结点

此外， 在到达一个结点的支配路径上的最后一个结点，记为直接支配结点（immediate dominator）， 如果一个结点记为n，他的直接支配结点记为m(m idom n)。在n的支配路径上，当支配结点不是自身时，支配节点d一定也支配m。

为啥要强调直接支配呢？要看我们表示流图中支配关系的数据结构： 支配树

支配树

首先，手工来找每一个支配结点的支配对象。此处我们的入口结点是1号结点， 我们可以看到，1号结点支配所有结点， 而2号结点在1号结点的分支上，下层所有结点都可以从3号结点到达， 因此2号结点仅支配它自身(任何结点都支配自身)。 如图，以此类推。如此生成一颗支配结点树。

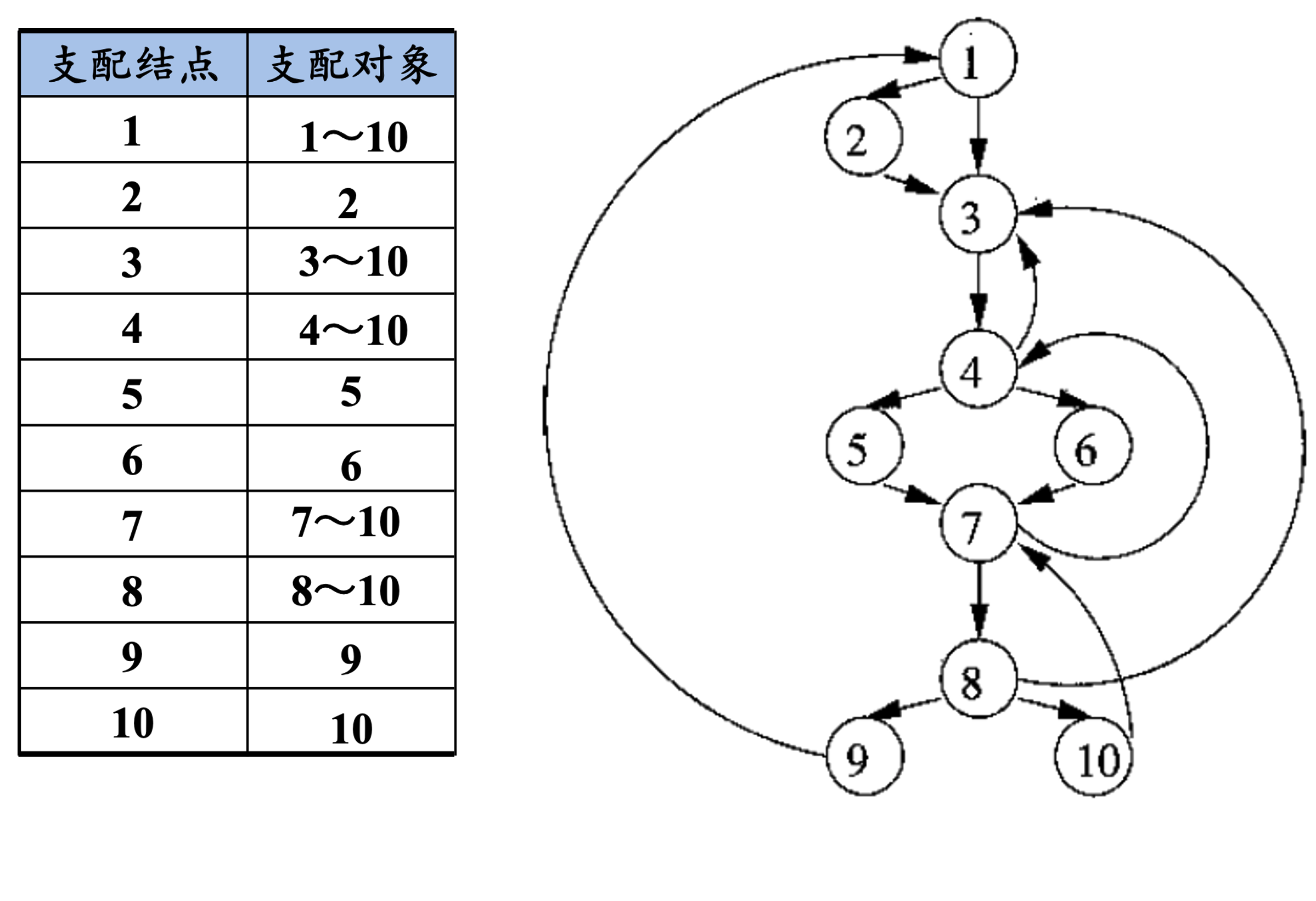
image-20201208181751573

这颗树上，入口为程序根结点，每个结点支配它的后代结点：

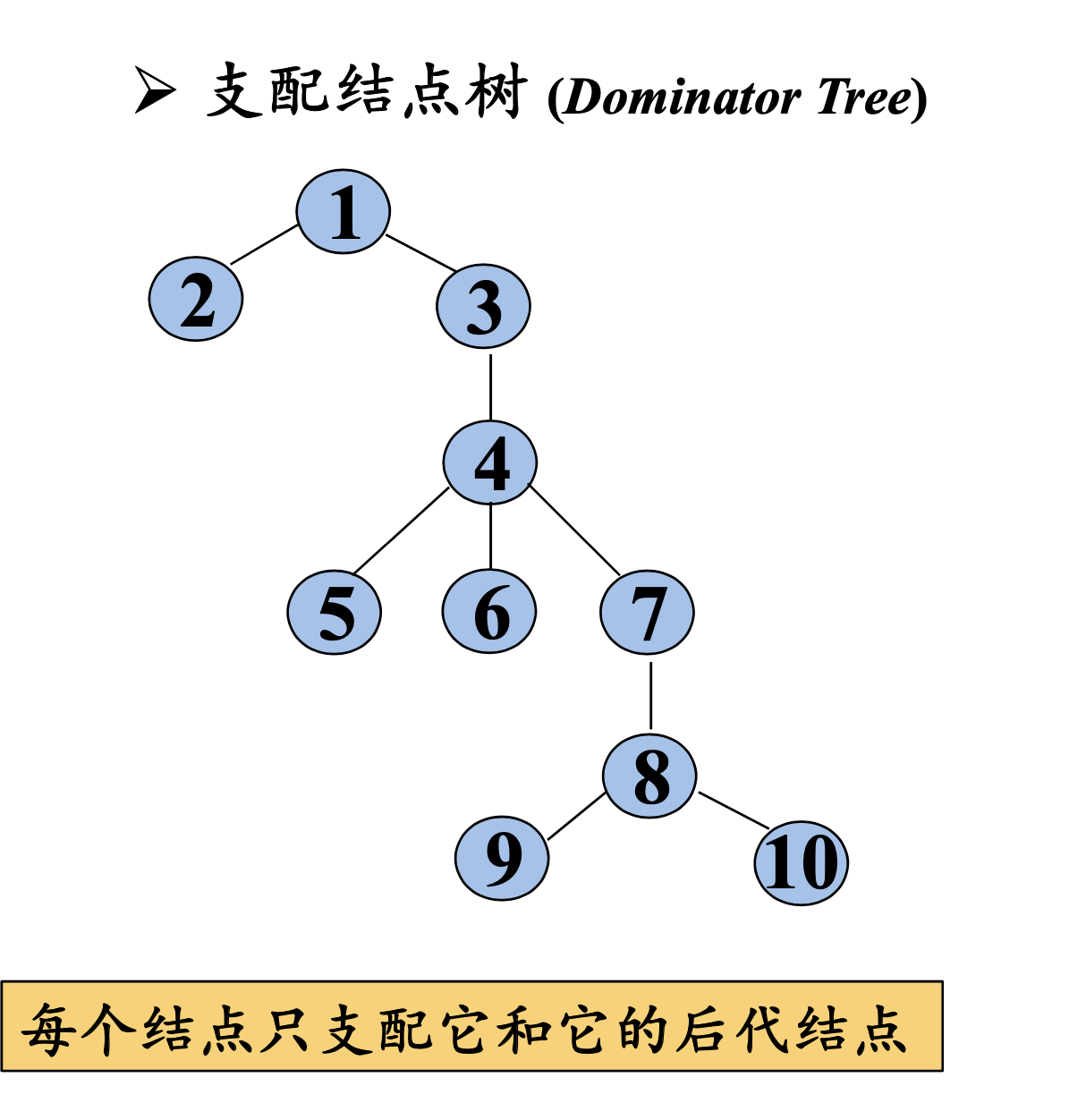
image-20201208182015843

生成树的性质：

  • 顶点： 程序入口点

  • 边： 直接支配结点

  • 路径： 所有支配路径

支配路径分析算法

要设计一个算法，来求出一段程序中每个结点的支配路径。 那么整个算法的思想如下：

如果p1,p2,p3....pk是结点n的所有前驱， 并且d不等于n, 那么当且仅当每个d dom pi时(pi为每个p)，d dom n。

也就是说，n的一个前驱结点如果要是称为n的支配结点d，那么必须支配到达n点的所有前驱。因此他表示成的数据结构也就是一棵树(回溯祖先只有一条路经)。

比如上面的程序流图中，4到8点之间有5，6，7三个点， 4号结点同时支配5,6,7,因此4号结点支配8号结点；而5号结点到8号结点之间有7号结点， 5号结点并不支配7号结点(他只支配本身)， 因此5号结点并不能支配8号结点。

好算法原理介绍完了，接下来我们设计这个程序分析。

截屏2020-05-17 下午9.56.10

对照这张表，分析次算法。

  • Domain: 基于抽象的数据集， 应该选择所有点

  • Direction: 求每个程序点的支配路径，Forwards更直观

  • May/Must: 为了保证我们的分析结果safe，那么这应该是一个must-approximation，以确保支配路径的唯一性。

  • Boundary: 边界条件，由于是前向的，Must分析， 那么程序的边界应该是OUT[entry]， 从上到下，而初始应该不是空集，而是本结点为支配结点(入口结点是所有结点的支配结点)，即OUT[entry] = {entry}

  • Initialization: 因为Meet是交运算，每个程序结点的初始化应该是所有路径OUT[B]=N(假设所有结点都是他的支配结点)

  • Transfer funciton: 每个基本块内的转移函数，因为是前向分析，所以转移函数应该IN[B]union上本身{B}。F(x) = xU{B}

  • 在merge处(程序数据的合并点)我们取交集。

image-20201206101945309

这个算法的Transfer function和之前的-kill +gen的不同， 需要注意。

拿来那张Must分析的图：

截屏2020-08-13 上午8.54.34

初始时所有前驱点都是支配结点，然后将这个集合不断缩小知道最大不动点，求最大下界。

因此我们的Iterative Algorithm有：

image-20201206102844236

来看具体的例子：

image-20201206104654556

D(n)是所有结点的支配结点的集合。

D(1)是入口结点， 支配结点就是它本身。

D(2)中的转移函数回吧IN[B]即D(1)union上自身{2} => {1,2}

D(3)同理， 转移函数{3}unionIN[B]，这里的IN[B]是有四条边， 根据merge取并集，我们有D(1)nD(2)nD(4)nD(8)因为4，8没有分析，所以他们的OUT[B]都是初始值，所有点。因此D3 = {1,3}。

停止条件：

因为我们的OUT[B]=IN[B]union本身，我们看第一次迭代后，其实已经达到了不动点。比如D(3)在第二次迭代时，D(1)是恒不变的，D(2)就是不变的。此时D(4) = {1,3,4}, D(8) = {1,3,4,7,8} 他们的并集一定是小于等于4的结点集合,即{1,3,4}，而只要有前驱1,2在，那么支配结点的并集就一定是小于3的。(不考虑环路)

如果不考虑环路了， 那么在无环图上，根据支配结点的性质， 除了入口结点，每一个结点都有唯一的直接支配结点。再比如4号结点，有3和7两个入边，要证明停止， 我们就要证明7号的支配结点一定包含{1,3}而不会再包含2，那么算法就停止了。也就是说只计算一次，路径中的所有支配结点都出现了，不会再添加其他的了。如果再添加了2，即{1,2,3}那么程序中到达4就会有两条路经，1，3，4和1，2，3，4。

如此一来， 算法变成了：

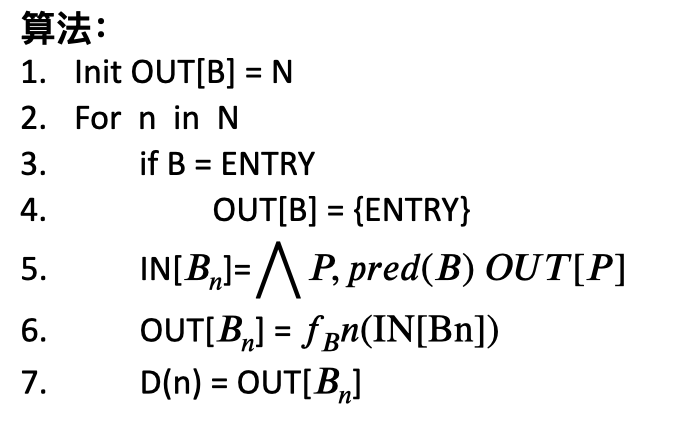
image-20201206113136795

没有了while循环。

2. 深度优先生成树

我们需要分析循环XD，现在，我们根据支配路径分析算法， 得到了生成树，也就是说得到了流图上每一个点的支配路径信息。而实际控制流图所走的路径中间夹杂着支配结点之外的结点。此外，要在流图中刻画循环，我们需要知道流图中什么时候前进，什么时候回退了。这些信息需要生成一个深度优先生成树来提供。

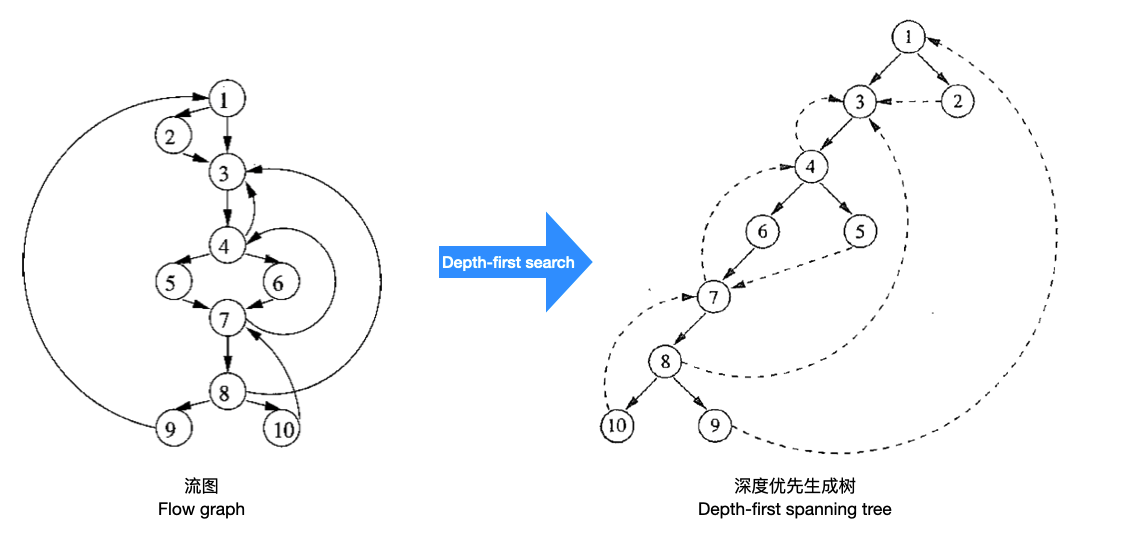
image-20201207105042417

要在流图上进行深度优先搜索所得到的序列: 1,2,3,4,5,6,7,8,9,10 。我们可以生成深度优先生成树， 这棵树的后序遍历序列(10,9,8,7,6,5,4,3,2,1)之反就是我们所需的序列。

实现这个算法：

image-20201207105419198

具体算法：

image-20201207105454286 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#coding=utf-8
'''
dfst
～～～～
'''
_visit = set()

_graph = {
        1: [3, 2],
        2: [3],
        3: [4],
        4: [3, 6, 5],
        5: [7],
        6: [7],
        7: [4, 8],
        8: [10, 9],
        9: [1],
        10: [7]
        }

_c = len(_graph)

def search(n):
    _visit.add(n)
    print(n)
    for s in _graph[n]:
        if s not in _visit:
            search(s)
    global _c
    _c = _c -1
    print("_c = {}".format(_c))

search(1)

output=>
1
3
4
6
7
8
10
_c=9
9
_c=8
_c=7
_c=6
_c=5
5
_c=4
_c=3
_c=2
2
_c=1
_c=0

如此一来可以看到：

image-20201208100007943

图中流图的边可以分为三种：

1） 实线边，即深度优先生成树算法生成的边，也就是前进边(Advancing edge)，这些边推进流图向下执行。

  1. 虚线边中从子节点指向其祖先的，也就是后退边(Retreating edge)，这些边指向上层。

3）另外一些虚线边(5->7, 2->3)，这些边互相都不为祖先。也即是交叉边(cross edge)。

3. 自然循环

回边

给了一个流图， 要对循环进行分析。首先，我们定义了支配结点这一二元关系。然后通过直接支配结点，我们构建了一颗深度优先生成树，在这颗树上，顶点就是程序入口点，边就是直接支配关系，所有的路径就是所有的支配路径。有了这层关系，我们在树上不上了虚边，在后退边中，我们现在定义一种回边。这种回边一定是后退边(但是后退边不一定是回边)。回边的定义是这样的如果1 dom 9 现在有一条边，他的头是9，尾是1那么也就是说尾支配了头，这就是一条回边。

上边说了，后退边不一定是回边，如：

image-20201208174753377

这是鲸书第七章的一个例子。从流图a中我们可以看到c和d的流形成一个环路， 但是他生成的任意一种深度优先生成树(或de在前或c在前)。都有一条后退边，指向一个他的非支配结点。

因为我们在第一步计算了一个结点的所有支配对象，在第二步计算出了流图的深度优先生成树。那么我们就可以拿到所有支配路径，以及支配路径上所有结点的支配结点信息。通过生成树，我们就可以知道流图上那一些边是后退边，通过支配结点的计算，我们就可以知道后退边指向的是不是支配他的结点，从而判断一条后退边是不是回边。

自然循环

如果一个流图中，他的每一种深度优先生成树中所有后退边都是回边，那么这张流图就是 可规约的（reducible），此时他每一种遍历情况下生成的深度优先生成树的所有后退边的集合，都是相同的。

自然循环定义：

  • 必须具有一个唯一的入口结点， 称为循环头(header)。
  • 具有一条进入循环头的回边。

image-20201208204910207

在此图中可以看到， 在流图中找自然循环， 首先，找出所有回边。

然后如4-3: 这歌循环中3号结点为循环头，找到所有不经过3而到达4的结点：

4， 5，6，7，8，10。 然后再加上循环头3就是这个自然循环的组成。

构造一条回边的自然循环：

image-20201208205823633

算法说明一下，注意两点，一是n初始的时候已经在Loop中了， 二是找的是栈顶指针的前驱，弹出后，有前驱再压栈。比如还是在4-3的自然循环中，我们第一次循环压入了4， 然后找到了前驱m=[3,8], 3是循环头不过if, 因此8被压栈；下一轮8出栈，7入栈；再一轮7出栈，5、6、10入栈。。。

所以说这里就是以循环头为上界进行一个流图的反向深度遍历。

自然循环性质

  • 除非两个循环有相同的循环头， 否则他们要不分离，要么嵌套。
  • 一个循环不包含其他循环称为最内层循环(innermost loop)/同理流图中包含所有循环的是最外循环
  • 下图中包含同一个循环头，很难说哪一个是最内循环(可能是循环中的if...else)，因此合并循环

image-20201208211513630

后记： 循环优化

补充虎书第18章循环优化的内容

Loop-nest Tree