7. Relate Iterative Algorithm to Fixed Point Theorem 4:20

8. May/Must Analysis, A Lattice View 26:10

9. MOP and Distributivity 64:30

10. Constant Propagation 80:40

11. Worklist Algorithm 102:00

    总结&欢迎谭添老师

南大静态分析6

上回说到为了解决iterative algorithm中的三个问题， 我们引入了数学模型来进行形式化证明。 那么如何让在lattic上呈现的fixed point theorem与iterative algorithm关联起来呢？接下啦我们来看。

首先回顾一下iterative algorithm的三个问题：

Review The Questions We Have Seen Before

我们现在尝试回答三个问题。

1. 算法一定能达到不动点吗？(lattice 上单调性问题)
2. 如果有不动点，只能有一个动点吗
3. 不定点是解吗

Relate Iterative Algorithm to Fixed-Point Theorem

04:20

将Iterative Algorithm这个算法与fixed point进行关联(一种很intuition的证明)：

• Iterative Algorithm

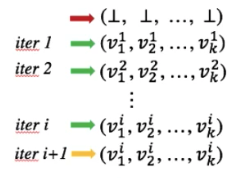
• Fixed point:

将二者的已知条件进行关联， 首先iterative algorithm 也需定义一个Lattice:

在算法的k-tuple中， 每一个节点对应一个Lattice, 那么所有节点形成的vector就是一个Lattice的product。 那么整个iterative algorithm作用的是一个product lattice。

• 在product lattice (L, L, L...L)中， 如果每一个L都是finite的complete lattice（complete lattice不一定finite哦），那么他们构成的product lattice也是finite的complete lattice。

  通过此条我们就可以关联上不动点定理的第二个条件： L is finite

现在我们来关联不动点定理的第一条件：f: L->L is monotonic, 如何说明，iterative algorithm也是单调的呢？

首先，iterative algorithm的function是什么呢？

如上所言，在每一次迭代中，都会应用一个function F, 他由两部分构成：

• transfer function: 指定的transfer function, 根据IN[B],来进行kill和gen

• join/meet function: 在控制流上，进入下一个program point之前的并/交操作

  e.g., F(iter1) = (v1....vk)

有了F, 接下来证明他是monotonic的：

首先第一条之前也说过，每一个transfer function在固定的program point上，由程序性质所决定kill和gen都是一样的， 所以他是单调的(OUT只会增加，不会减少)。

再来证明第二条：

这里的LXL是两条控制流path在进入program point之前进行merg, 也可以有多个(Actually the binary operator is a basic case), 我们只需要证明这个basic case是单调的就可以了。

我们来证join是单调的：

根绝我们之前对单调函数的定义:

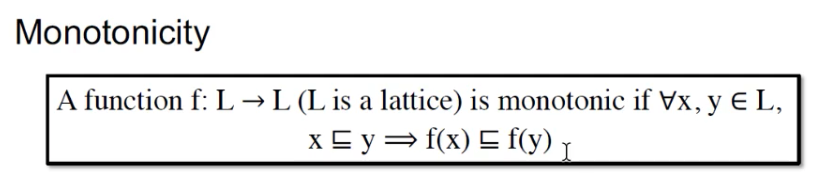
此时的function是一个join(U)操作， 因此，我们的function是证明:。

join在lattice求的是任意两个元素的最小上界(least upper bond)，那么yUz是y的upper bound，同时也是z的upper bond。根据upper bound 的定义得到:, 根据偏序关系中的传递性，我们就可以得出: , 然后得到完整的证明:

因为根据join(U)的定义, yUz是y和z的一个upper bound，那么y <= yUz。 之后通过偏序关系(<=)的传递性得到: x<=yUz。因此，yUz就是x,y,z的一个upper bound。

根据join的定义xUz是least upper bound of x and z。 那么根据最小上界(least upper bound)的定义： xUz <= yUz。(最小上界“小于等于”任何一个上界)。

因此，现在将fixed point theorem的两个条件都和iterative algorithm有所关联了，那么就可以使用fixed point theorem 来说明之前提到的iterative algorithm for data flow analysis 上的问题。

给出两个结论，我们的iterative algorithm根据不动点定理：

1. 算法保证一定能够达到fixed point
2. 达到的fixed point 要么是greatest fixed point, 要么是least fixed point
3. 探讨algorithm的一个复杂度的问题，如果前边两条成立，那么什么时候算法才能达到不动点呢？

为了说明第三点，首先引入height of a lattice的定义：

The height of a lattice h is the length of the longest path from Top to Bottom in the lattice.

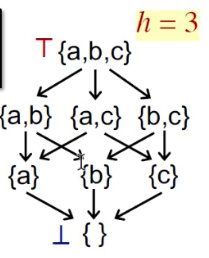
Lattice的高度就是从top到bottom找最长的路径，上图中是h=3。

第三个问题，就是说 The maximum iterations i, 最多的迭代次数，使得算法达到不动点(最坏的情况)。

做一个假设， 每次iteration, 在lattice上的每一步都做一个最微小的变化： lattice只移动移一步(相当于每次只有一个node变化， 且每个node中只有一个0变成1)。

每次都只变化一个节点，将一个0变为1，那么最坏的情况就是遍历所有节点，将所有位由0变成1：

最多就有h*k次iterations。

因此回答第三个问题：

May and Must Analysis, a Lattice View

26:10

映射

将一个power set做一个直观的映射

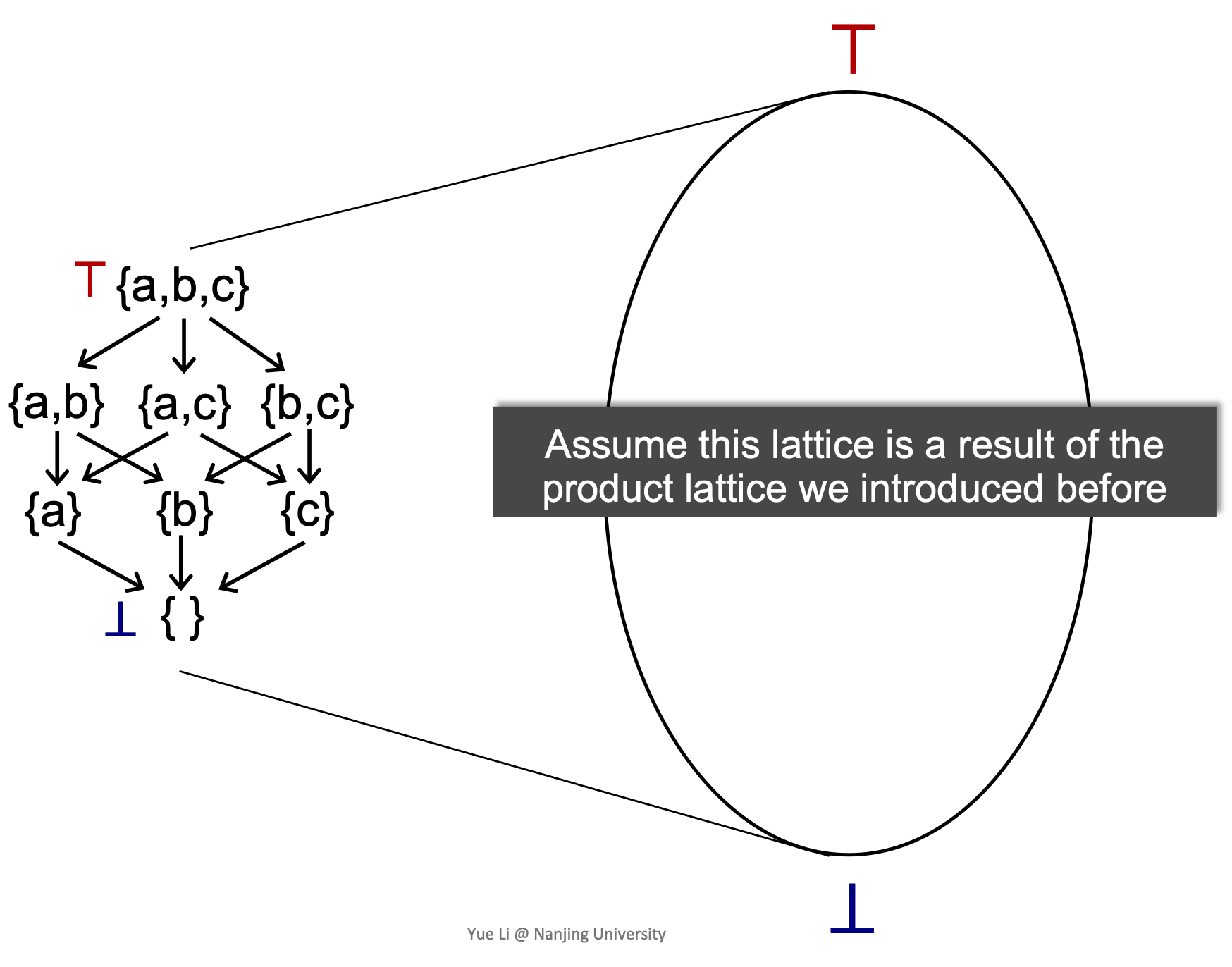
这里假设this lattice is a reuslt of the product lattice, 因为每一点都有一组k-tuple, 每一个点他都是一个lattice元素，我们要更新的是所有值，所以他是一个product lattice。

May

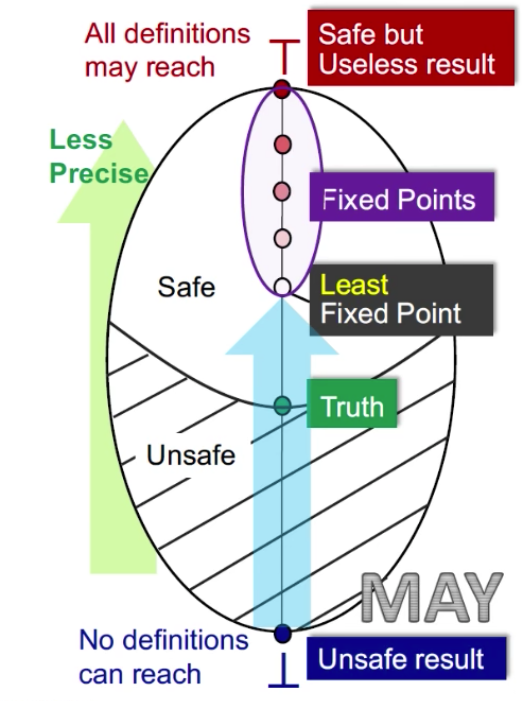
May analysis, 一般情况下是从bottom往top走， 一个lattice的bottom从may的角度来讲，就是一个unsafe result。 也就是说，

无论是 may analysis 还是 must analysis都是从unsafe的result向safe的result来讲的。

• Unsafe result : 为什么May analysis的unsafe 是在bottom呢？ 以 reaching definition为例， no definitions can reach 意味着对于每一个variable, 都没有任何一个defintion能够reach到。

• Safe but useless result: 以reaching definition为例，表示对于每一个variable, 所有的definitions都有可能reach。他是safe的，但是没有用。

我们想知道，我们的分析停在unsafe result 和safe but useless result 中间的某个值， 我们需要引入另外一个值： Truth。

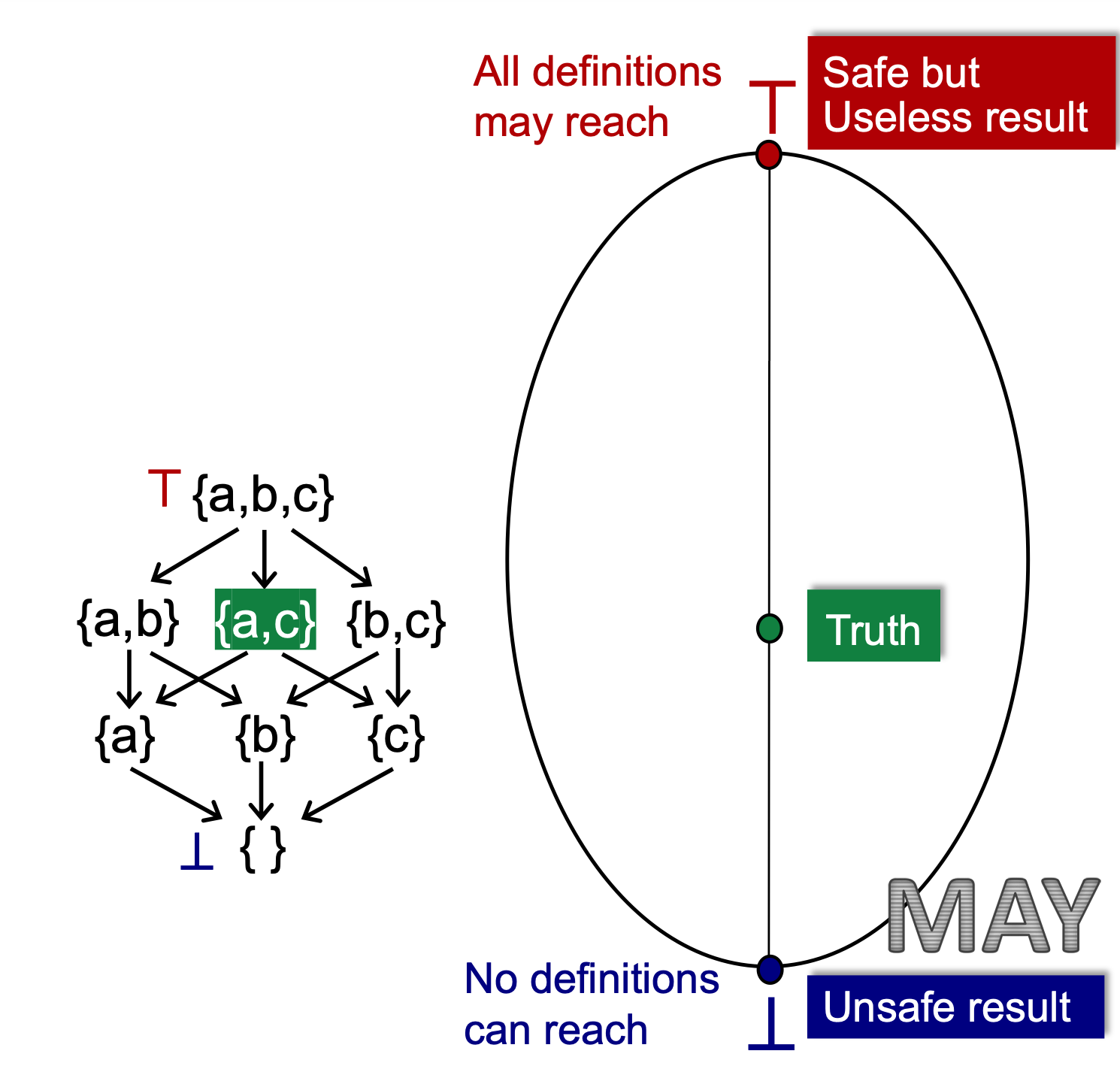
Truth, 程序动态执行时无论在什么样的书如下所有可能取得值的一个动态值的集合。

假设Lattice 上{a,c}是一个Truth的集合。 那么就可以画一条边界，如果是May的分析，就把a和c都包含。

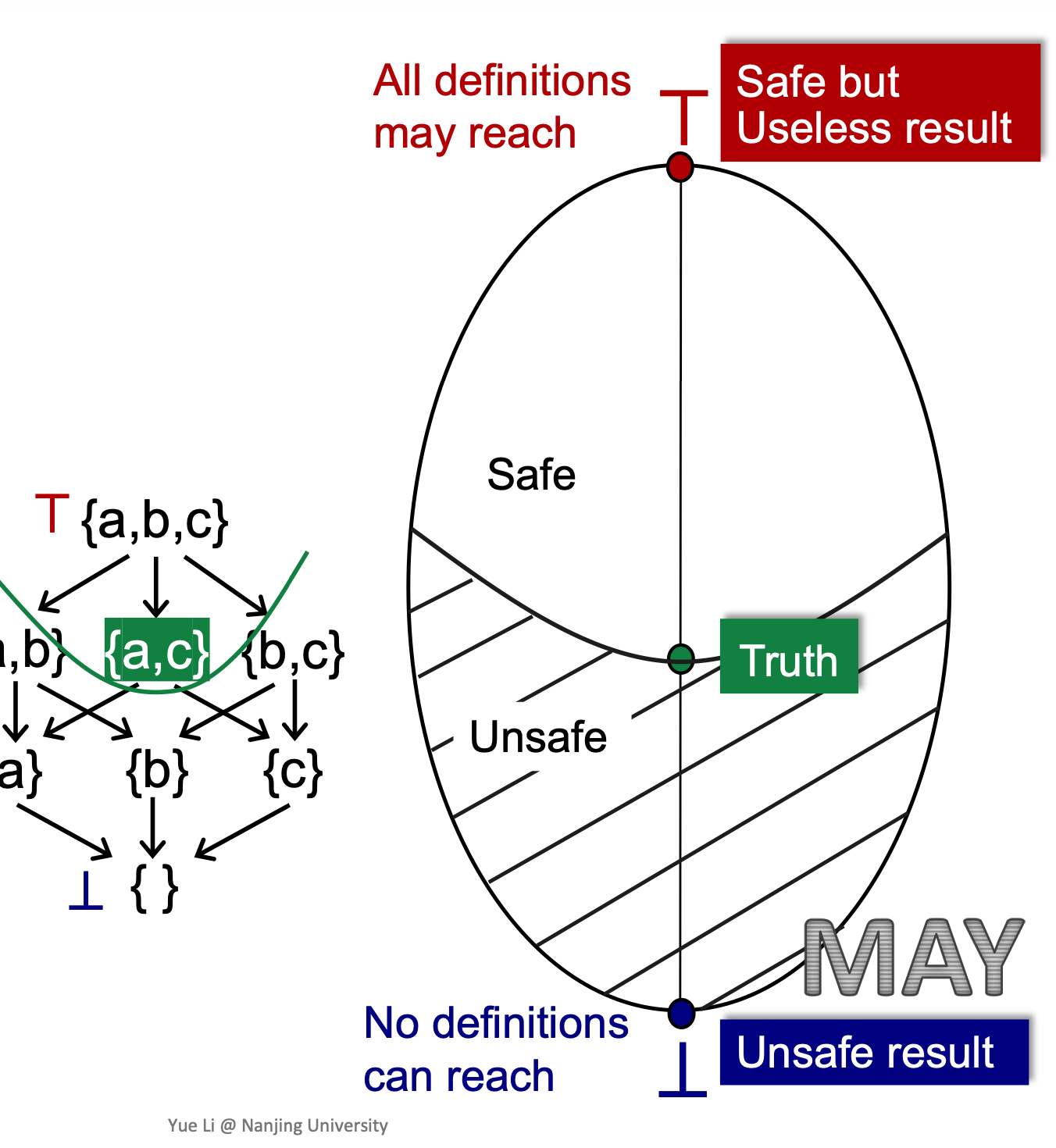
如何知道我们的分析会进入safe呢？

静态分析有两个要素：

1. data abstraction
2. safe approximation

我们在设计一个静态分析时，将merg与transfer functie 设置成safe的，也就是说，我们的设计保证了我们的分析结果一定会超过Truth这一点。

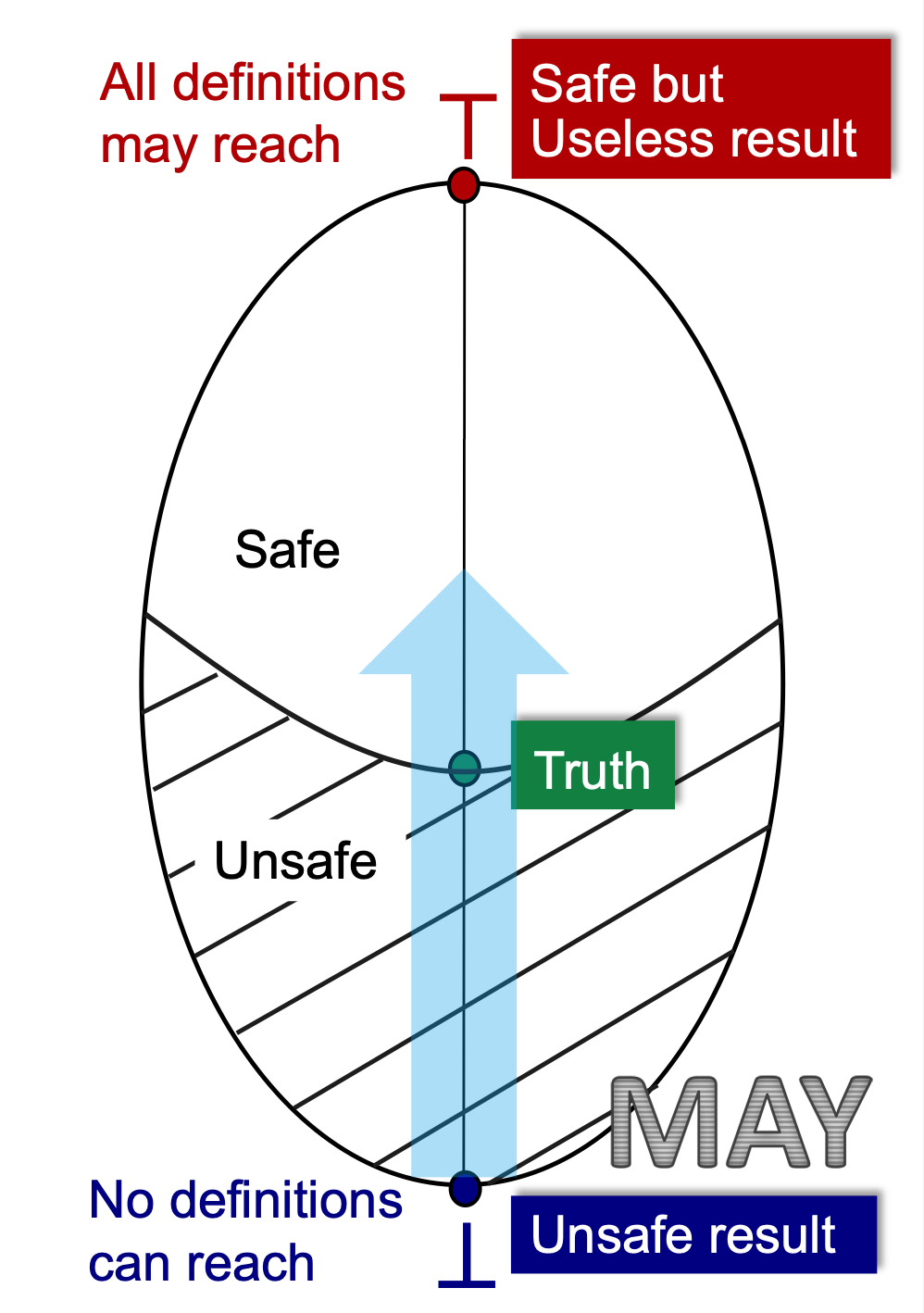
进入safe之后何时停呢？

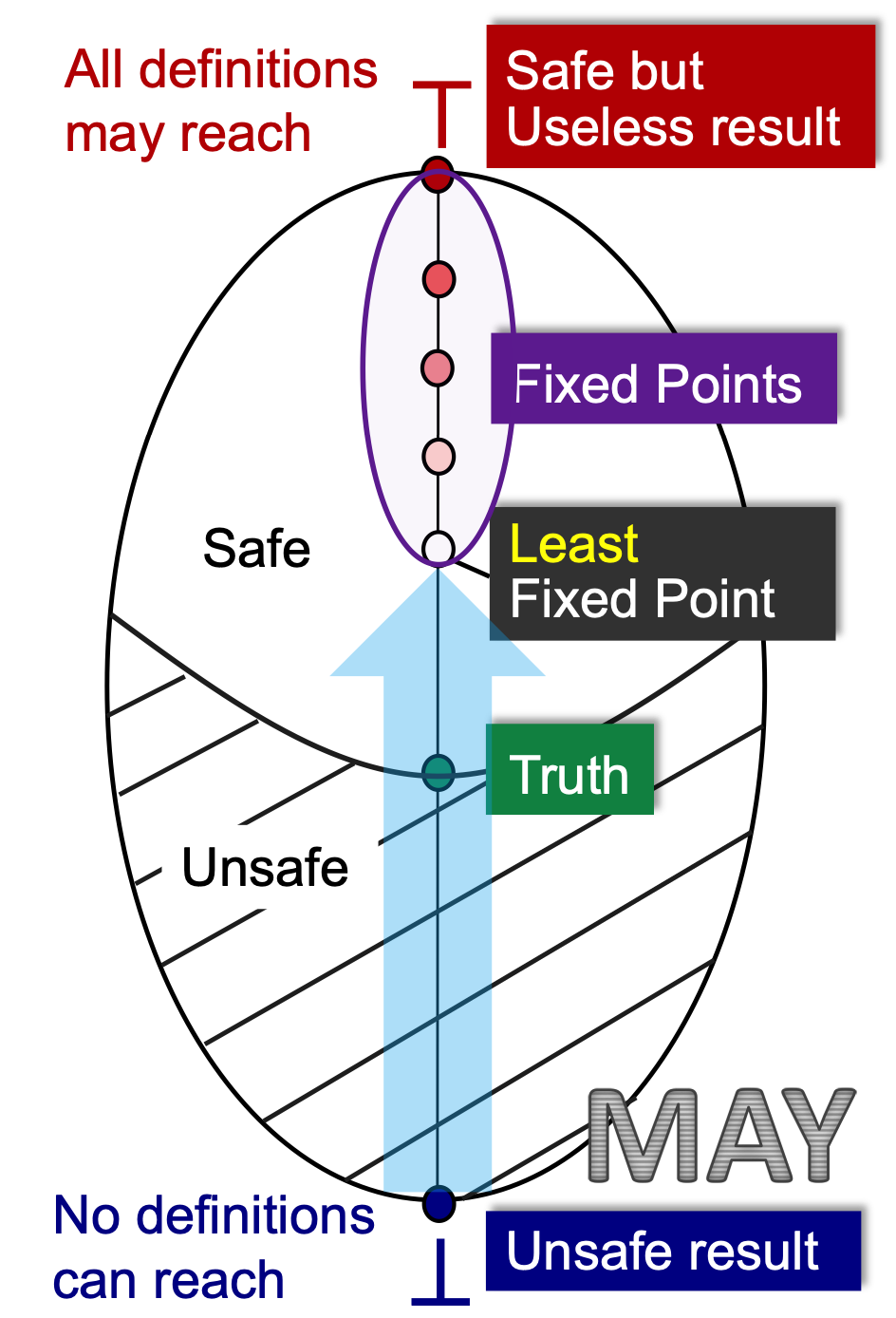
我们的不动点可以有很多，但是虽然有很多不动点， 但是我们使用iterative alogrithm求解出的不动点，由我们之前给出的证明，iterative alogrithm求解出的不动点，一定是最小不动点(least fixed point)。

那么我们得到的结果精度如何呢?

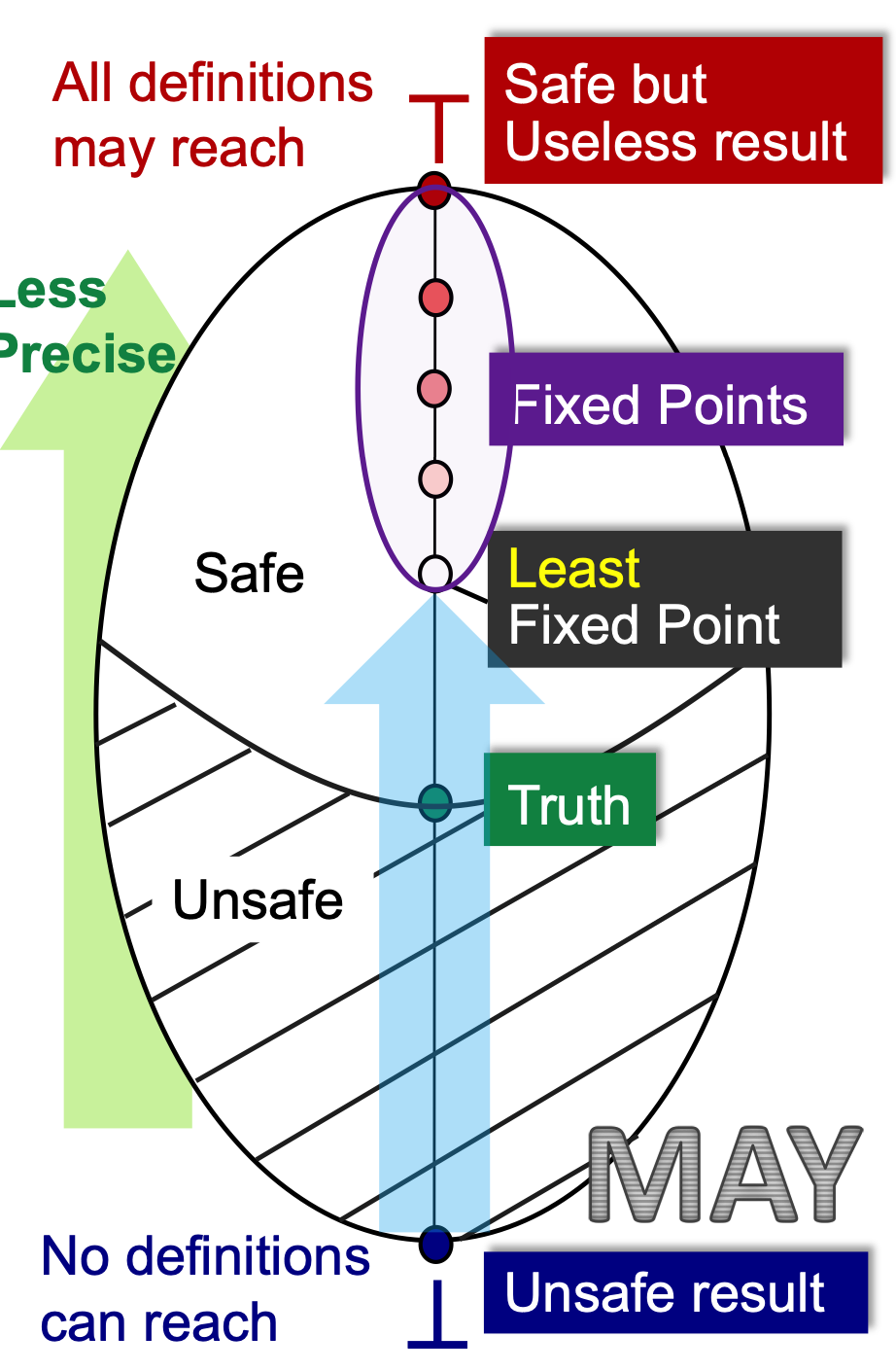
无论是may还是must分析， 都是从准到不准走。 如上图，越往上的不动点越不准的，因为我们使用iterative algorithm能达到的是leaset fixed point, 那就是你能达到的所有结果中，最准的。这就是为什么一旦达到不动点，但是我们达到的fixed points里最准的(但他不一定是truth)。

MUST

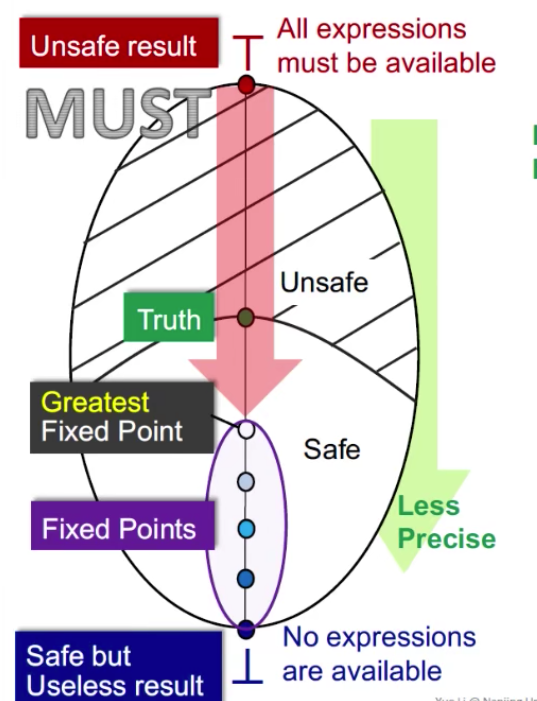
Must和May相反，一般是从Top(unsafe result)往下走到Bottom(Safe but unless result)。

以available expressions为例，他是一个must analysis:

• Top(unsafe result): 所有的expressions在某一点都available，结果unsafe。
• Bottom(safe but unless result): No expressions are available, 么有expressions可以被重复利用， 所以是safe的，但是 没有用。

在must analysis中， unsafe就是有误报的情况。 Must Analysis是top-down, 他根据iterative algorithm 走到的fixed point一定是greatest fixed point(就是最准的)。也就是说针对must analysis而言我们往下走到的greatest fixed point一定是最准的。

Safe approximate 中safe是先满足的条件，能达到fixed point是后满足的。

合照：

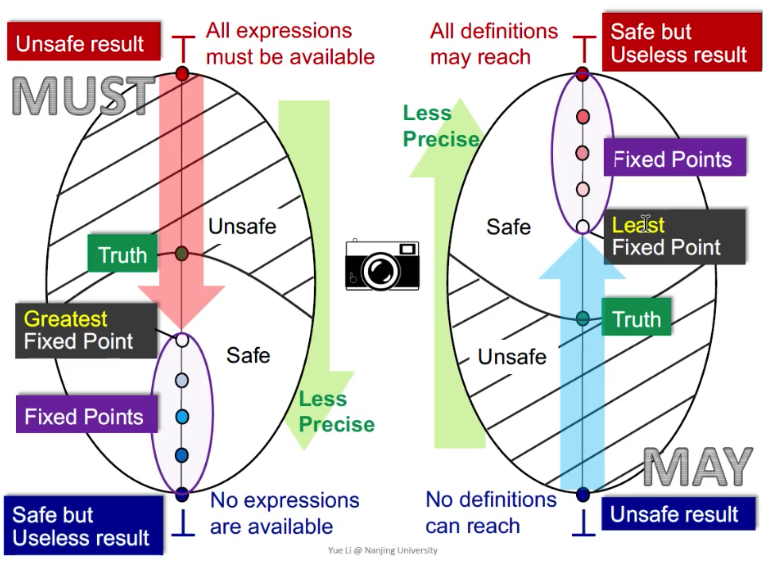
How Precise Is Our Solution?

64:30

谈到精度的衡量， 我们就需要一个方法：

MOP: Meet-Over-All-Paths Solution(MOP)

其中，meet也包括了join, 就是所有分支汇聚到一点的情况。 具体就是：

在control flow graph 中 path就是从entry开始一堆statement构成的Path； 有Path就有Transfer function Fp:

就是这条流上每一点的transfer function 的composition。

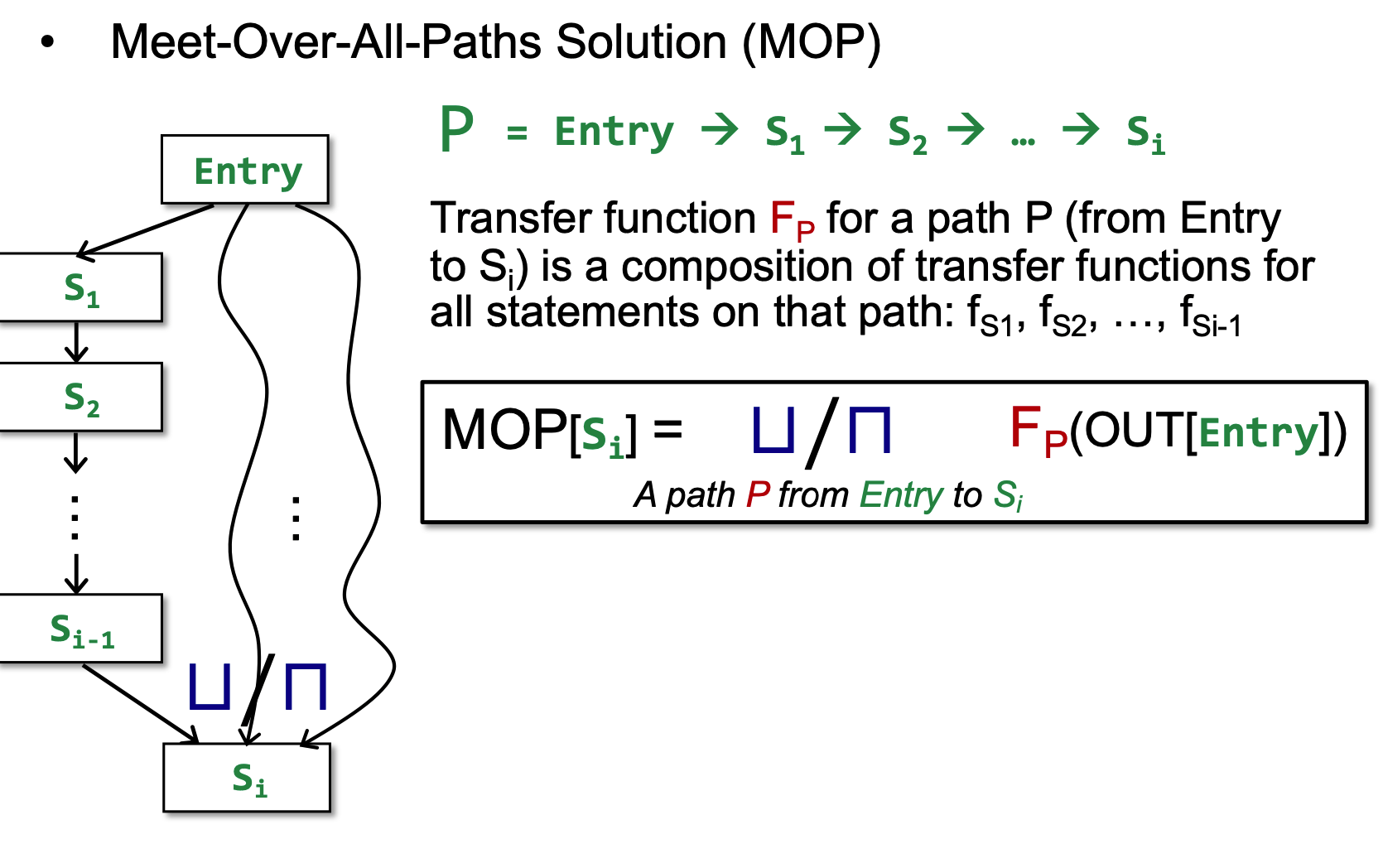
MOP(Meet-Over-All-Paths Solution)就是枚举从Entry点到Si的所有path, 然后对每条Path应用Fp， 并将得到的结果join/meet起来：

• not fully precise: 观察一下，所有的paths, may be not executable（动态运行时，无论什么输入之下都不能走的路径），在MOP中merge了此类路径，就是误报，所以就not fully precise。

• Unbounded, and not enumerable: unbound就是说如果有循环的话，静态不可知循环终止(无边界)； not enumerable: 大型程序中，路径可能不可枚举的。

  

所以我们静态得到MOP其实是impractical的。

Iterative Algorithm vs. MOP

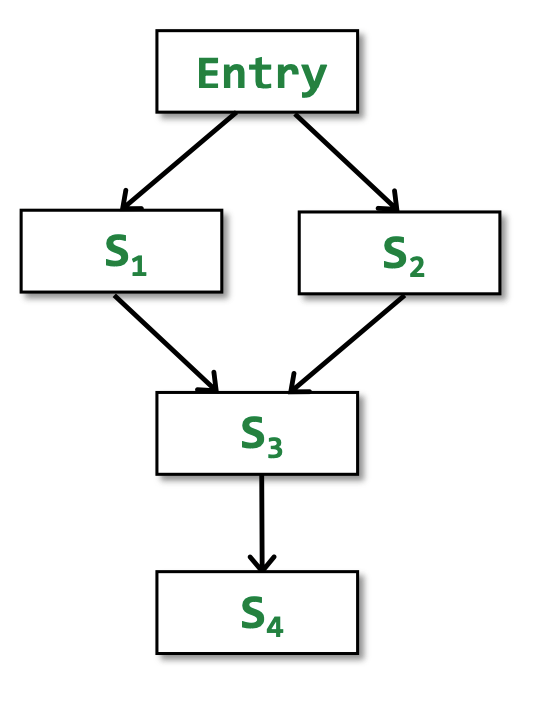
如图， 我们要求S4点的IN:

使用iteractive algorithm, 在所有merge的时候，用join:

而使用MOP(meet-over-all-paths)的方法，是在每条path都算法之后，对每条path进行join:

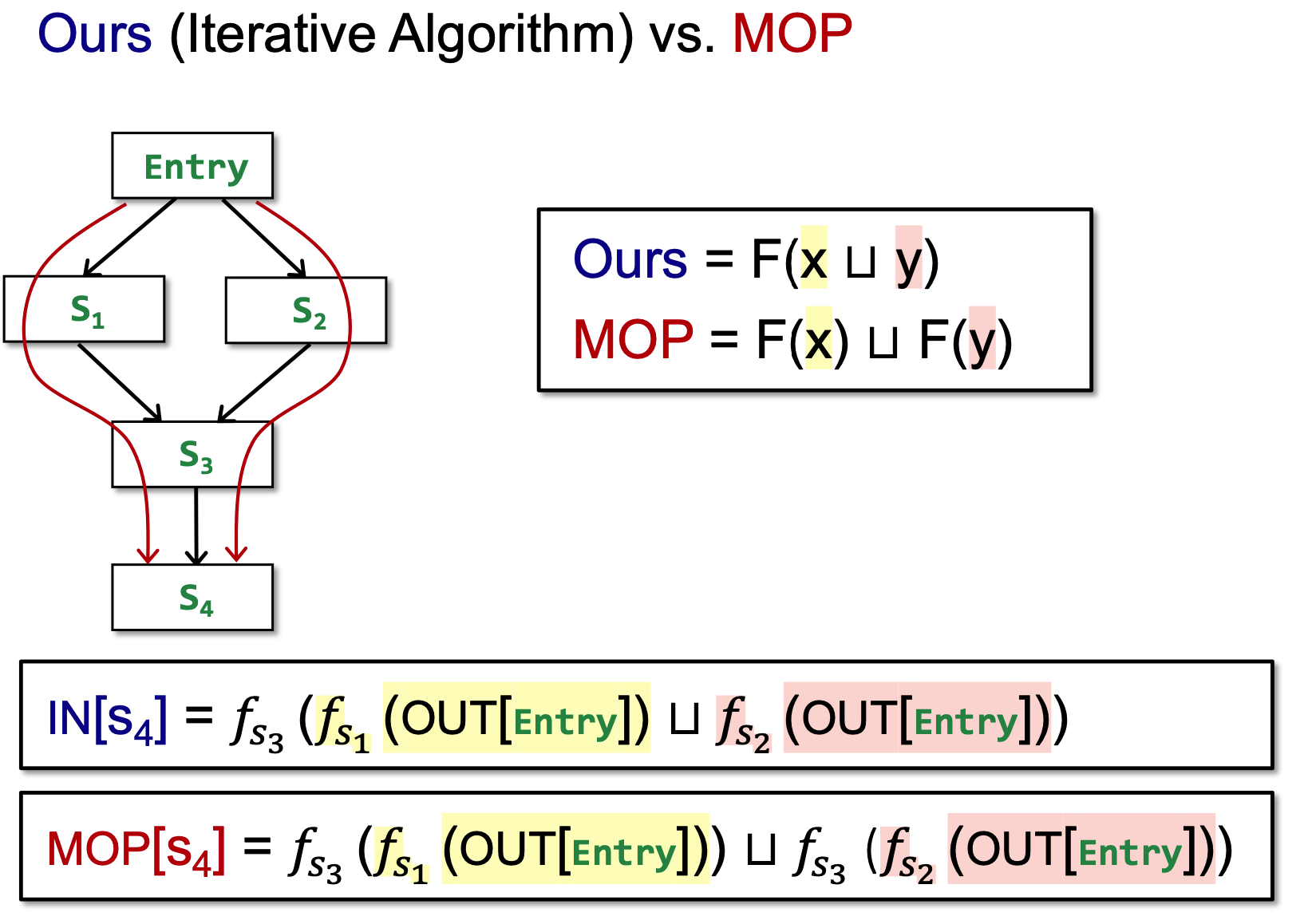
上图我们可以看到，红色部分和黄色部分iterative algorithm 和 MOP其实是一样的，我们进行抽象：

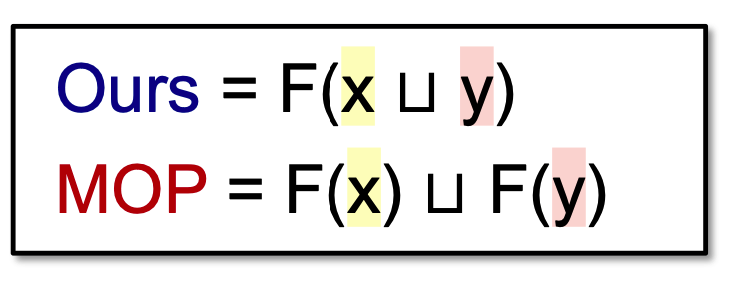
iterative algorithm和MOP有什么关系呢?

证明:

• 根据最小上界(least upper bound)定义, 我们有： x join y即是x的上界又是y的上界 (x<=x u y and y <= x u y)。
• 因为一个transfer function是单调的，我们有：
• 

根据偏序关系， 这就意味着F(x u y) 是F(x)和F(y)的upper bound。

• 因为F(x)uF(y)是F(x)和F(y)的least upper bound, 所以我们有:

  

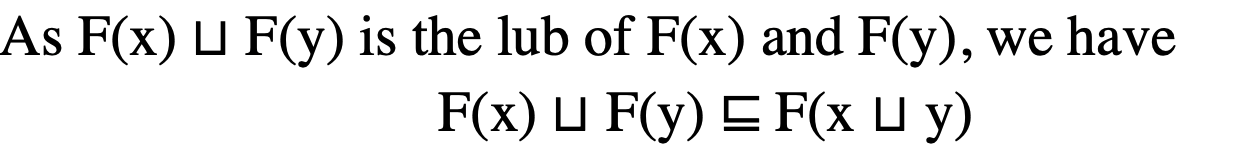
• 左边就是MOP右边就是Ours => MOP <= Ours

因此， MOP更准。

上边证明出的MOP和Iteractive Algorithm(Ours)满足一个偏序关系， 那么偏序关系有一个自反性， 如果满足自反性，那么Iteractive Algorithm就可以和MOP的精度相同。

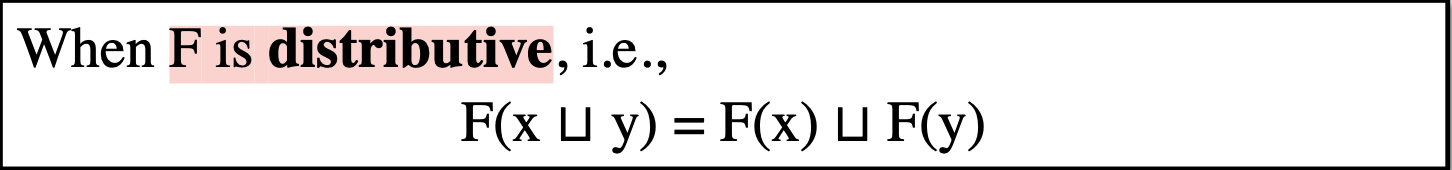
当Function是一个distributive(可分配性)的，就可以和MOP一样准：

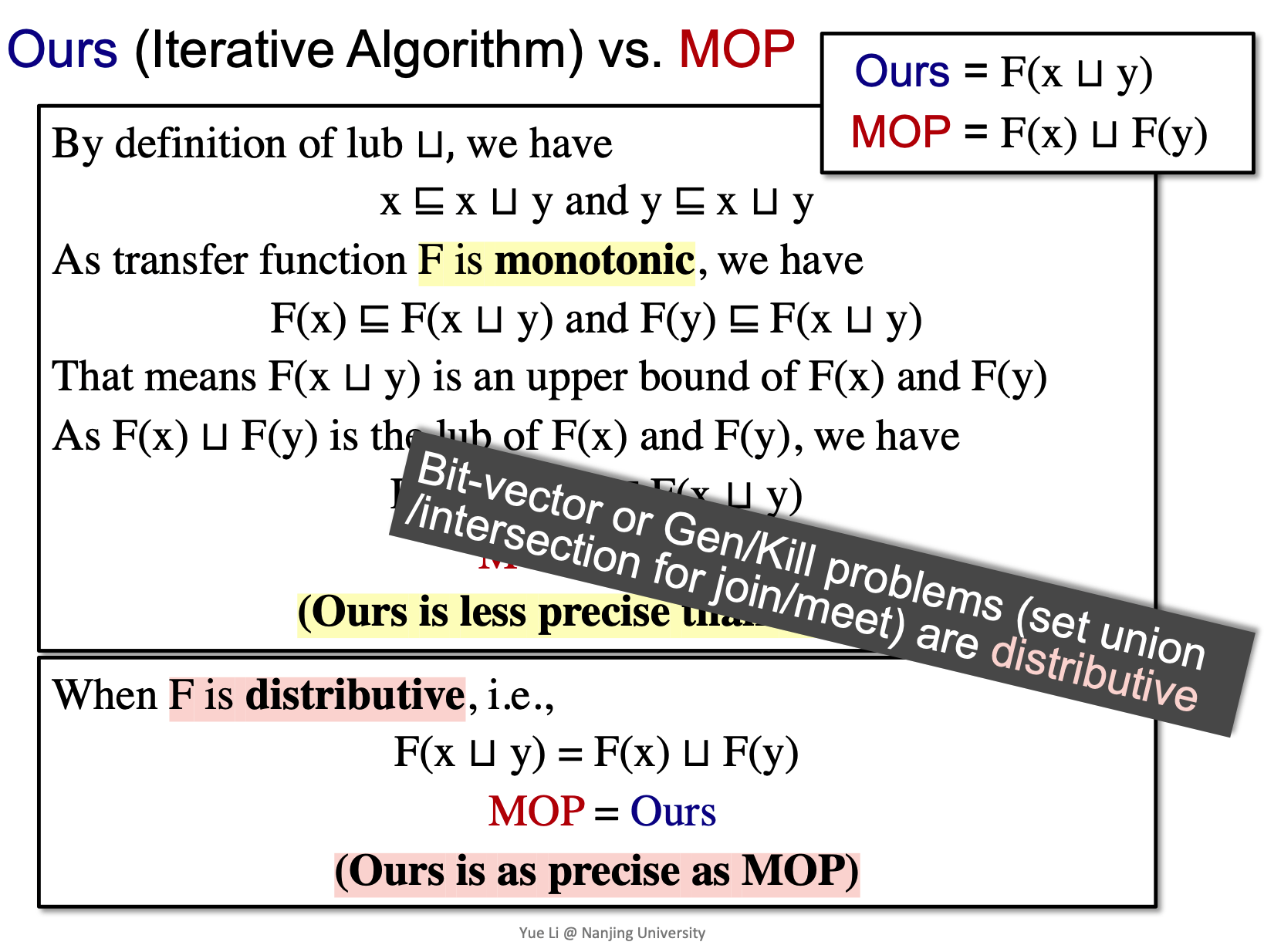
之前的4个分析，都是distributive的； 这样一类操作都可以叫做Bit-vector problems(or Gen/Kill problems)

这里一类问题的集合操作都可以用集合的union和intersection操作

Bit-vector problems都是distributive的。

那么有没有不是distributive的呢?(MOP更准)， 这里介绍了: Constant Propagation常量传播问题。

Constant Propagation

Define:

Given a variable x at program point p, determine whether x is guaranteed to hold a constant value at p.

一个variable在某一点，是否保证x一定指向某一个常量。

• The OUT of each node in CFG, includes a set of pairs(x, v) where x is a variable and v is the value held by x after that node.

这里的data flow的每个点上是一个个的pairs, 他代表了variable与value的对应。

设计一个Constant Propagation的data flow analysis framework我们接下来考虑他的方向，格和transfer function:

• Data flow direction: 数据流的分析方向是前向的。

• Lattice:

  

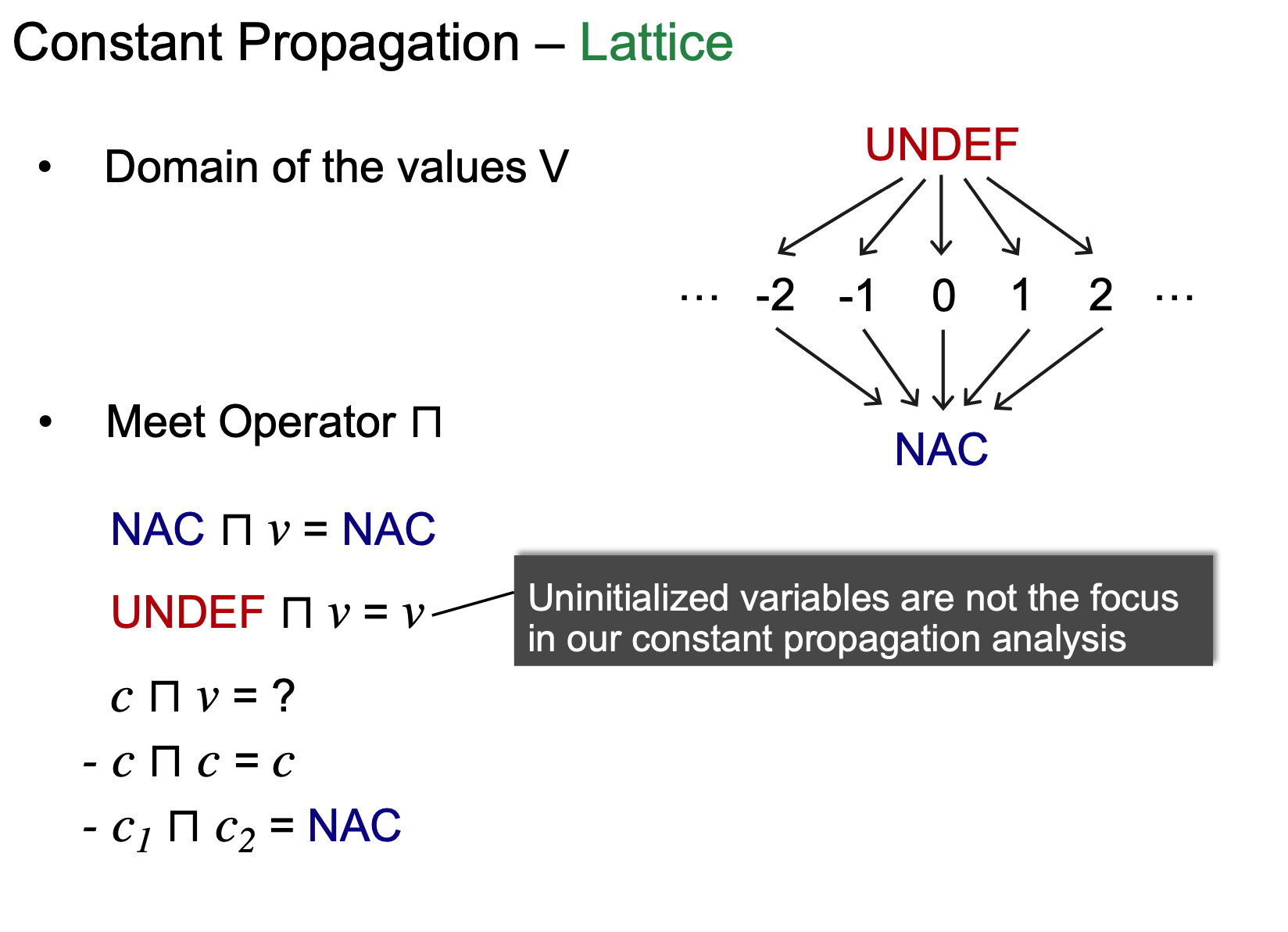
Lattice 来考虑两个构成部分: Domain of the values; Meet Operator。

首先看Domain:

• Bottom: NAC- 所有的variables都不是constants(safe but useless)
• Top: UNDEF-因为我们的元素是一个个的pair, 初始时variable指向undefine

再来看Meet:

• NAC n V = NAC， 不管V是啥，因为时safe的，汇聚点一定是NAC

• UNDEF n V = V， 这里说明一下，一般一个data flow analysis只负责一件事情，这里虽然有uninitialized variables的问题（汇聚后undef的值变成v了）。但是在以constant propagation为目的分析中，不影响。

• c n v 分两种情况，如果常量相同就是c, 不同就是NAC

总结：

再来看Transfer Function:

Transfer Function中，比较特殊的是{(x, _)}, 因为元素是一个pair, 所以这里_是一个通配符，表示x无论指向什么，都会减去。

我们用val(x), 来知道val指向的值：

• s: x = c; gen{(x, c)}, x就指向c
• s: x= y;(非constant), val(y)
• s: x = y op z, 二元操作： 如果y, z 有一个是NAC，就是NAC， 有一个是UNDEF, 就是UNDEF, 如果两个都是常量val(y) op val(z)

注意transform function只影响assignment statement。

下边说明contant propagation 不是distributivity:

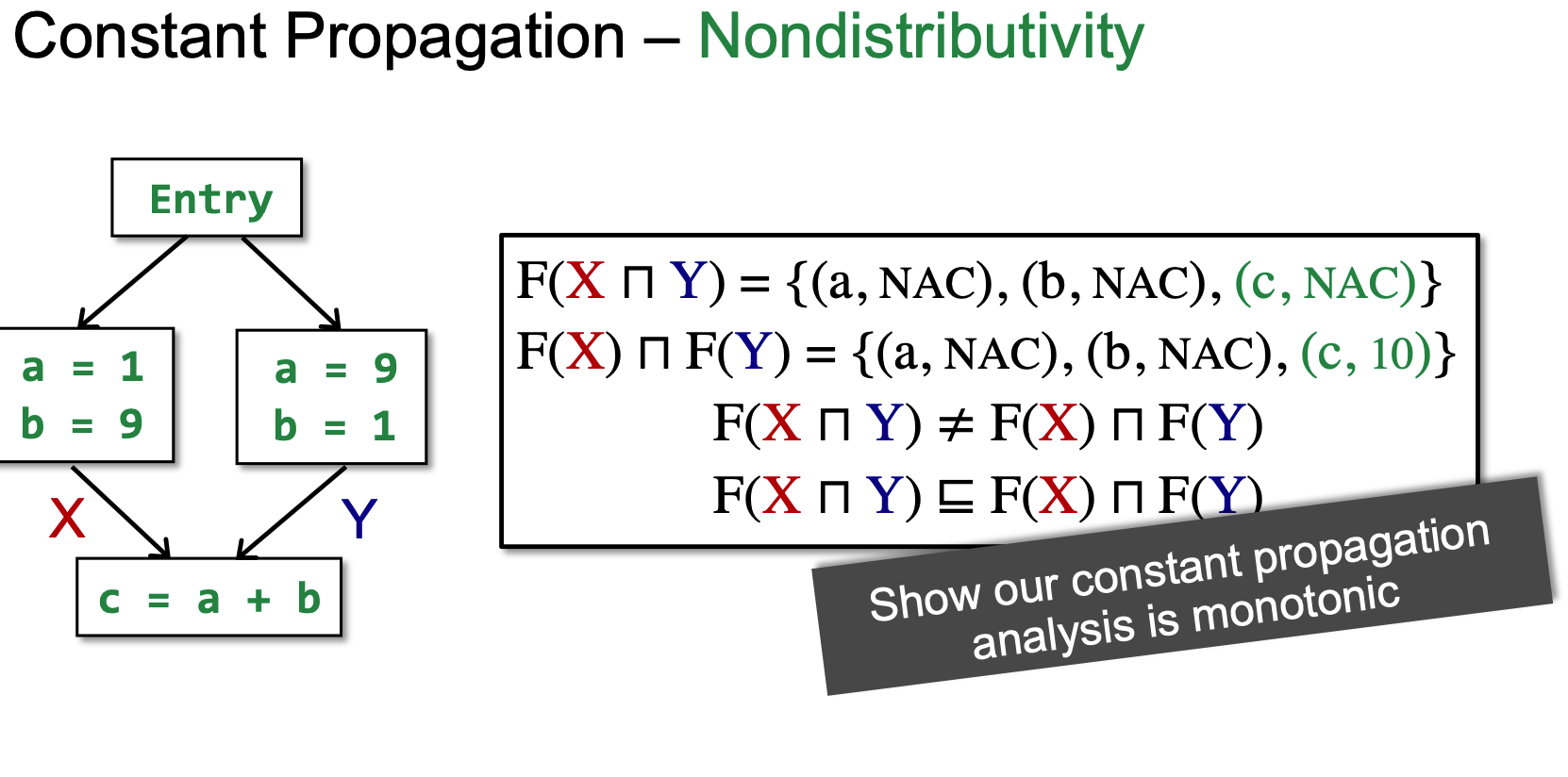
可以看到，F（XnY）时C是NAC， F(X)nF(Y)时C是10。

从Lattice上看，此例中NAC在10下边，所以在这个must analysis中越往下越不准的，所以MOP更准一些。

Worklist Algorithm

worklist algorithm是iterative algorithm的一种优化。

在实际工作中，不会用iterative algorithm, 而worklist algorithm更实用一些。

这里的终止条件要求，只要有一个basic block变化，就要让所有的basic block 都跑一遍，会有很多冗余。 而worklist的核心，就是只对那些可能变化的BB执行transfer function：

黄色的是新增的， 我们每一次迭代用新的out和之前的out比较， 如果一个out变了，那么意味着所有后继(successors)的IN变了。 我们就讲所有后继的B加入Worklist，就可以避免了大量的冗余计算。✌️～