- Iterative Algorithm, Another View 13:00
- Partial Order 27:50
- Upper and Lower Bounds 38:10
- Lattice, Semilattice, Complete and Product Lattice 48:40
- Data Flow Analysis Framework via Lattice 65:40
- Monotonicity and Fixed Point Theorem 74:30
1. Iterative Algorithm, Another View
The general iterative algorithm produces a solution to data flow analysis

这是通用的Iterative Algorithm, 思想是假设在一个程序生成的CFG之上,有k个节点,这个算法就会迭代的更新每一个OUT[n](节点的out信息)。

在值域V之上(就是我们待分析抽象出的domain),那么可以定义一个k-tuple 他的每一个元素是每一个节点的OUT[n],那么一次迭代分析 ,就是要更新这个集合中的值。

那么每一次迭代处理就可以理解为在这个集合上,使用我们为了达成目的所设计transfer functions(program point处使用)和control-flow handing(汇合处使用),来做更新(两种操作一个工作合称F来形式化表述)。F的输入输出为域(即上述集合)

当F的输入输出不再变化(相同),停止迭代。

图示:

将算法分为了三个部分:
红色代表初始化:
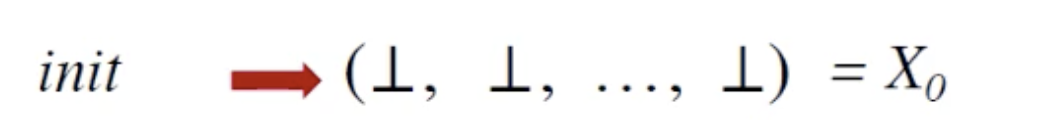
然后初始化每个位为bottom。进行迭代(绿色部分):
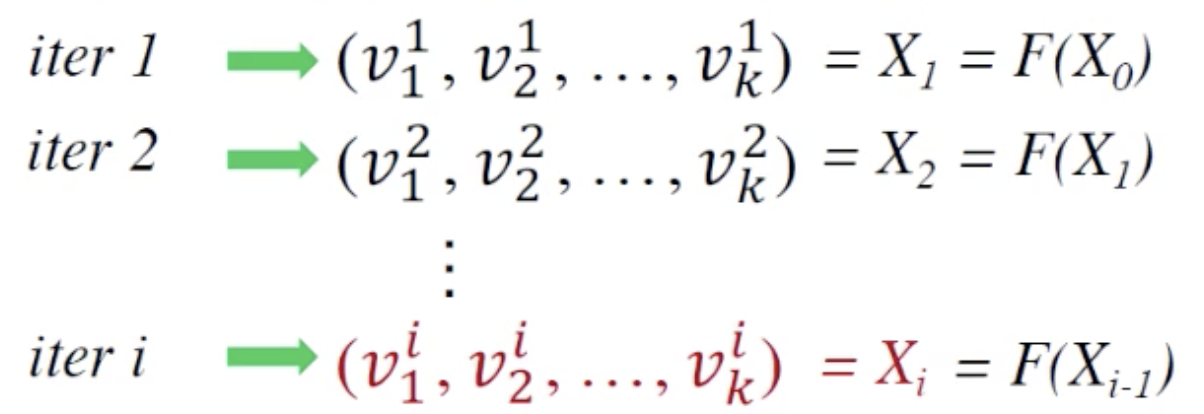
每次更新状态,知道状态不再变化,符合了停止条件(黄色部分):

这里的i+1 与 i 的k-tuple值相同。
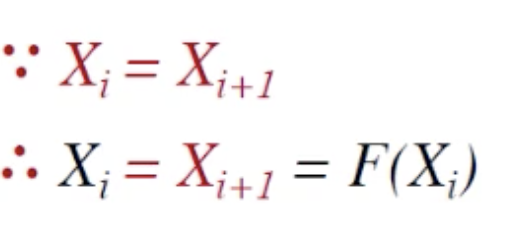
(所以X是F的不动点, X=F(X)(就像之前分析中,输入一个k-tuple(X)后不变了,算法停止))
2. Parial Order
首先定义偏序集:

偏序集:
partial ordering就是一种偏序关系,可以理解为部分之间的关系(集合中不要求任何两个元素之间有关系)
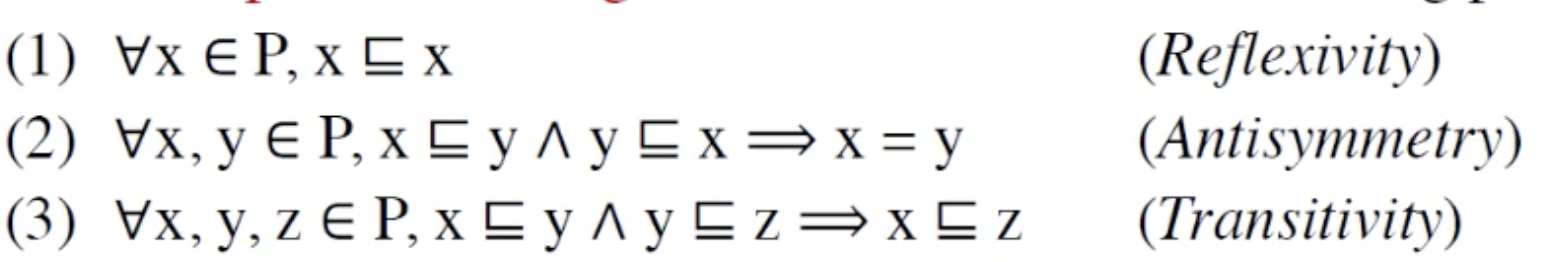
这三个性质:
Reflexivity(自反性):任意元素,关系可逆
Antisymmetrry(反对称性): x偏序于y 且 y 偏序于x => x=y
Transitivity(传递性): ...
小于等于符号: 偏序关系。
- 例子一:

S这个set是一个整数集,他可不可以是一个p(偏序集)?
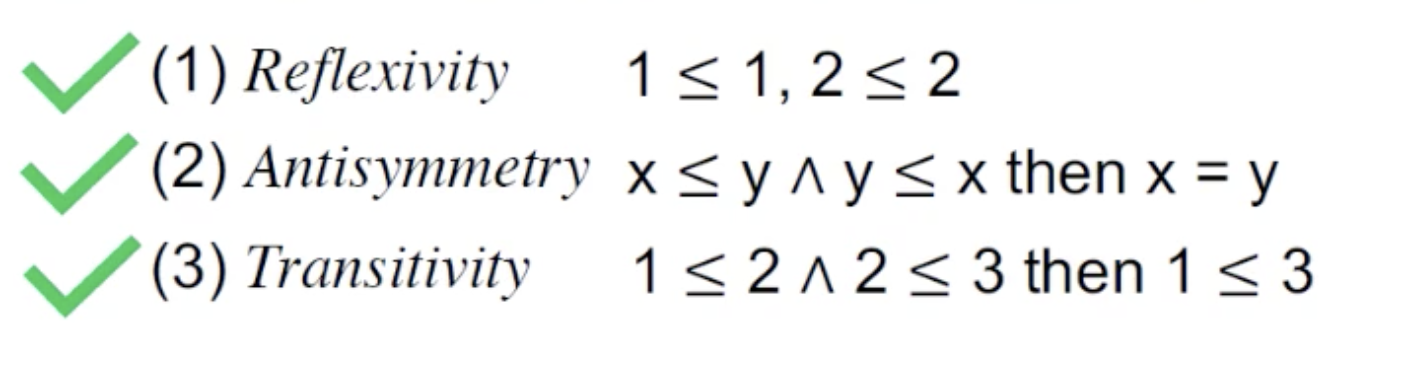
由三条性质,是一个偏序集。
例子二:
还是整数集set,但是偏序关系改成了小于:
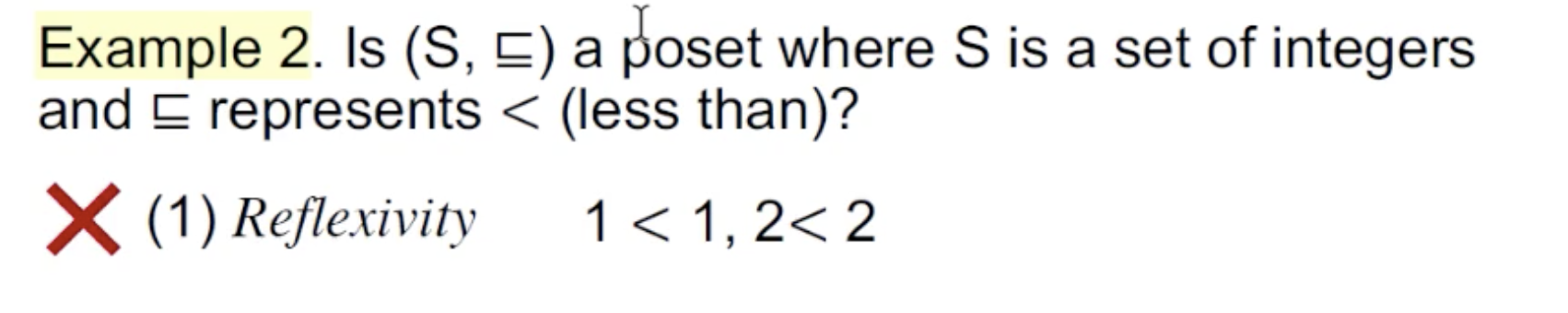
不满足偏序关系。
- 例子三:

字符型集合

符合,上边文字在强调偏序(partial)的意义。
例子四:
这个比较重要,每一个元素很想我们维持的状态抽象。然后箭头是控制流。。。

Upper and Lower Bounds
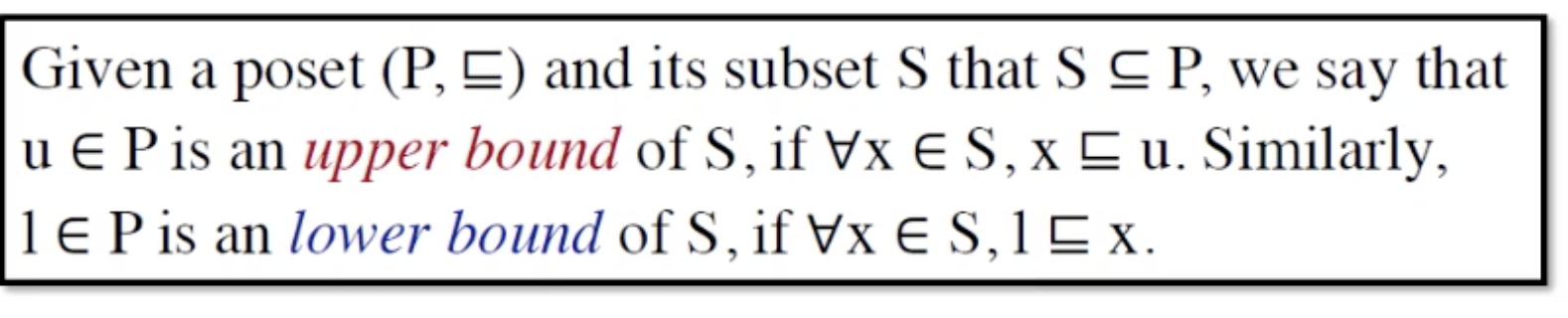
upper bound 上界

偏序集合P中取一子集S,这一子集中任意元素都属于或者包含的(偏序于)。这是对于子集的一个定义,而upper bound 和 lower bound可以有多个, 定义least upper bound和greatest lower bound


譬如这个子集, 他的upper bound可以是{a, b}也可以是{a,b,c}

一个符号表示:

关于lub和glb的性质:
- 不是每个偏序集都有
luborglb

- 如果有,一定是唯一的

(证明: 如果有两个glb,根据glb的性质,有那个公式,然后再根据parital order的反对称性,那么就是他本身)
Lattice


就是说如果一个偏序集的最大下界和最小上界都存在, 那么这就是一个Lattice。
- 例子1:

这里我们去从整数集合中取一个子集(取集合就意味着划定了边界)。那么他会有glb和lub。
例子2:

这里的S就是所有的这些单词, 可以看到pin和sin没有上界。 虽是偏序集也就够不成一个格。
- 例子3:

这玩意就是一个格
Semilattice
半格, join半格(有最大下界)和meet半格(有最小上界)

Complete Lattice

比格的定义还要严格,格是要求偏序集中任意两个元素有最小上界和最大下界;全格要求任意两个子集有最小上界和最大下界。

- 例子1:

这里一个整数集合中,虽然任取两个数字是有边界的,但是任取两个子集不一定有边界,如正整数这个集合,他是正无穷的。
- 例子2:


每一个有穷的格,都是全格。
数据流分析一般关注的都是全格,因为程序运行通常是有穷的
Product Lattice

就像iterative algorithm中的k-tuple, 每一个点的L都是一个Lattice。那么整个Ln就是一个Product Lattice



Data Flow Analysis Framework via Lattice
将前边Lattice形式化的定义应用在Data Flow Analysis上

通用性的Data Flow Analysis 表示:
一个数据流分析, 需要根据需求设计以下三个方面
D: 沿着CFG的数据分析方向
L: 就是那个值域集合,用
Lattice来表示,实际中,在入口点,要么是并集join,要么是交集meet。(根据safe-approximate决定) (所以龙书用了半格?)F:transfer functions, 每一个node都有自己的
transfer function
例子: reach definition :
- 正向分析, 看到s1, s3的out分别是{a}, {b}, 分别体现在左边流图和右边格上对应的黄色区域。
- Safe-approximate: join并集, 体现在绿色区域,在格上又上升了。
- 每个点转移函数后,生成out,在格上又上升了,到达上界。

may analysis 在格上是往上升的
一句话概括:

Review The Questions

算法一定能达到不动点吗?(lattice 上单调性问题)
如果有不动点,只能有一个动点吗
不定点是解吗
首先回答第一个问题:

实际上回答一个lattic函数的单调性问题。
Monotonicity&Fixed-Point Theorem
对于不动点定理的证明, 首先来看函数单调性的定义:

一个function在lattice(阈值)上是单调的,就是在域中任取x,y,都能够使得 x<=y => f(x)<=f(y)。
再来看不动点定理:
给定一个complete lattice如果:
Lattice上的函数是单调的,
L是有限的(一个finite lattice一定是complete lattice; 一个complete lattice不一定是finite lattice)
那么我们能拿到,function迭代到不动点一定是最小不动点(或最大不动点)。

需要证明Fix point是存在的并且是最大(小)的不定点:
- 证明不动点存在:

- 因为f单调,f(bottom)也是lattice上的值,且bottom<=f(bottom)。(bottom最小)
- f(bottom) <= f(f(bottom)) = f^2(bottom) (x<=y, f(x)<=f(y))
- 迭代...(上升链)
- L是finite,所以肯定存在一个k值,(最差情况下走到top),当fk(bottom)=fk+1(bottom)那么就到达了不动点。(因为Lattic是finitie的, 就限制了上升(下降)链是finite的)
- 证明Fix Point是最小(大)的:

假设存存在另外一个不动点x, 使得x = f(x) (不动点定义),定义bottom, 我们有bottom<=x;
使用数学归纳法:
初始条件: 因为f是单调的,f(bottom) <= f(x)
假设f^i(bottom) <= f^(x),那么我们根据monotonic有: f^i+1(bottom) <= f^i+1(x).
得到结论: fi(bottom)<=fi(x)
因为fi(bottom)<=fi(x)=x, 所以得: f^Fix = f^k(bottom) <= x(从bottom走到第k次的不动点一定小于不动点x)
将格上的数学证明关联到Iterative Algorithm,就可以证明我们的iterative algorithm是存在不动点且是最小(大)的了:

下节课进行关联...