前言:
reaching definitions, live variables和avaliable expressions 都是可以表示为对一个bit array( bit map, bit set, bit string, or bit vector)迭代求解。 如reaching definitions, using a bit for a definition position in the program. 因此这一类问题也称 为Bit vector problemshttps://en.wikipedia.org/wiki/Data-flow_analysis。
Live Variables Analysis: 06:10
Available Expressions Analysis:
总结:
Live Variables Analysis(活跃变量分析)
May analysis
活跃变量分析, 如果一个变量v在程序点p开始的路径里被使用过,那么在这条路径上,变量v就是一个Live Variables。 这种分析常常用作寄存器优化,将那些从某一程序点不活跃的变量(即之后不再使用的变量),做为寄存器替换对象。

- v在路径上被使用过
- v没有被重定义
目标抽象
关注的抽象应该是live variables,即活跃变量。我们设立一个数据结构来表示程序中所有的变量活跃状态。

比特位表示状态,比如有100个variables,每一个比特位代表一个变量。形成bit vector, 每一个program point上分配一个(bit vectors)。 有了抽象的状态表示,接下来做safe-approximation制定transfer function 和control flow analysis来操作这些状态位。
方法设计
我们的程序在流动之后,如何变换我们的标志位,使得我们得到的结果safe?
即如何设计transfer function和control flow 合并。
分析方向
前向分析和后向分析都是可以的, 但是在live variables的分析中, 我没每个program point的bit vector表示的是路径上所有变量在之后是否被用了,如果是forward分析的话, 从entry点开始向下,我们在每一个program point上不能确定每个variable是否在之后的语句中被use了, 此时如果再往下走,发现某一个variable被use了,那么需要向上传播这个消息来通知之前program point此变量在后边被use了。 但是backward的话,从exit开始进入,先找到的是variable的use点,后找definition信息, 因此变量被use了这个信息就可以随着后向数据流propagate, 从而节省了开销。
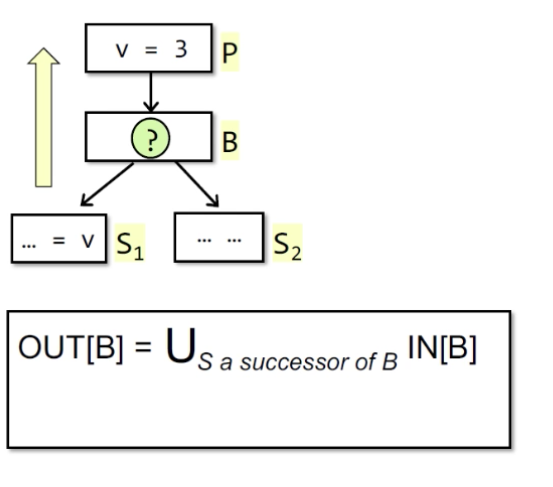
汇聚点处理
看这里在BB[P]处有一个v=3 的表达式,BB[B]不知道。而在BB[S1]处用到了v, 在backward中走到BB[B],BB[S1]和BB[S2]汇合,看图中抽象公式,要处理在merge处的近似,因为是may analysis所以使用Union。(不放过任何一条path)
然后就是核心的设计Transfer function:
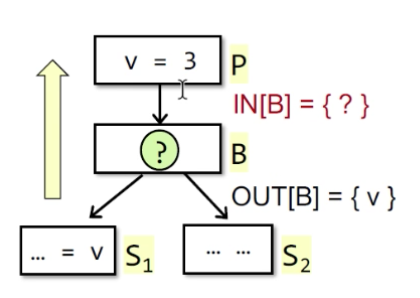
刚才我们说过, 在此数据流分析中, 我们采用backward, v在BB[S1]中被使用了,且在汇合处,我们做union操作,所以得到有OUT[B] = {v},现在在程序中, 我们要backward过一个条任意语句(假设Baisc Block中只有一条statement,即以单条statement为分析单位)。我们要设计transfer function,得出上出program proint处的IN[B],即OUT[B]->IN[B]。

这里有一个场景,现在v=3寄存 器R中待着,经过我们的live分析,如果走过该点,经过我们设计的transfer function,IN[B] = { v }, 那么这个值就在寄存器里待着。如果IN[B] = {},那么就把它从寄存器中拿出。因为我们的目的是分析数据流中,变量的live情况,由前面的定义如果BB[P]处的变量v是live的:
- BB[B]中v被使用过?
- BB[B]中v没有被重新定义?

因为我们是在backward分析IN[B]这个program point的状态,来决定v=3是否被寄存器丢掉,即IN[B]这一点的事关v在未来是否会被使用到。看在第一个情况中,与v无关,但是我们知道OUT[B]这一点我们union出了OUT[B]={v},因为是backward分析,即接下来v会被使用到(BB[S1]处)。那么这一点中,v没有被重新定义,那么IN[B]={v}
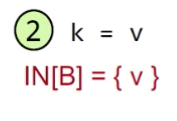
这里面v被使用了,离着v=3更近,这种情况下,即使OUT[B]={},也会有IN[B]={v}。

这里v=2,v是lval左值,那么这个defition中v被重新定义了,上边v=3就不live了,因为没有被使用过,就被redefine了。此时IN[B]={},依据这个状态,从这个program point开始,寄存器中的3可以拿掉了。
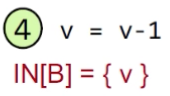
再想象一下寄存器中的那个3,v=v-1中,右边的表达式是一个使用了寄存器中该值的二元操作。因此在这一时刻,我们需要使用寄存器中的3,那么IN[B]={v}。
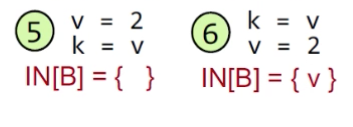
这里case5是先写后读,case6是先读后写。在先写的时候 ,寄存器完全可以舍去3 。因为没有用到,还要重新读,而在case6中,寄存器中的3先被user了一下,所以在被redefine之前,有use,就是live咯。
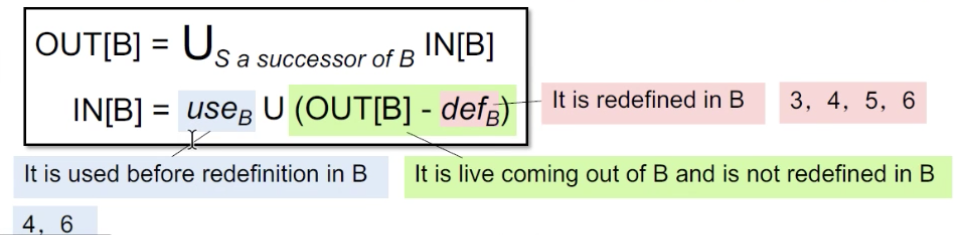
这里就定义了经过BB时的transfer function。
设计好了,就开始用算法动起来。

这里的定义,我理解的是因为transfer function是从下往上一句一句走的,那么先走到define被删掉了,然后use就又加上了。所以正序来看,先use后define就是live的。
INPUT: CFG
OUTPUT: 每一个program point的标志位的状态
METHOD: 第一句的边界条件,因为是backward的,所以是IN[exit],这里设置是空。(未来没有变量会被用到了)。然后所有BB初始化为空,求到所有的IN[B]不回被change了(反向)。
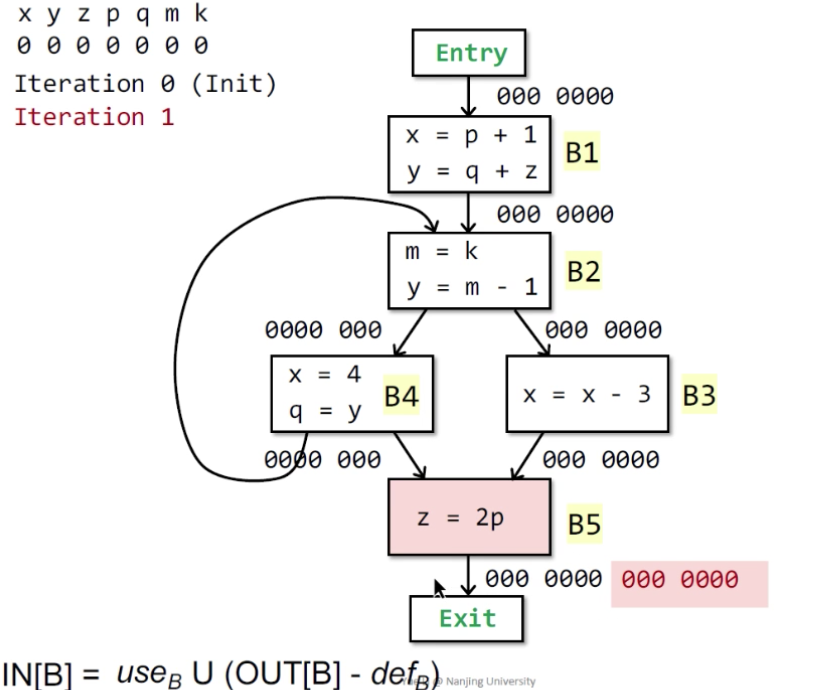
STEP:
- 抽象7个变量位7个特位
- 分配给每一个program point(IN处),并初始化为零。
- 第一次迭代(backward)开始
- B5:
z=2p,p被use加上,z被redefine删除=》0001000 - B3:
x= x-3x 先被use后被redfine,需要加上=〉1001000 - B4: B4的OUT需要先union一下两个后继节点(successor)的IN,即(IN[B2]+IN[B5]),然后transfer =》 0101000
- B2: IN[B4]+IN[B3] = 1101000,加m,减y,加k,减m => 1101001
- B1: +q+z-y+p-x=>0111001
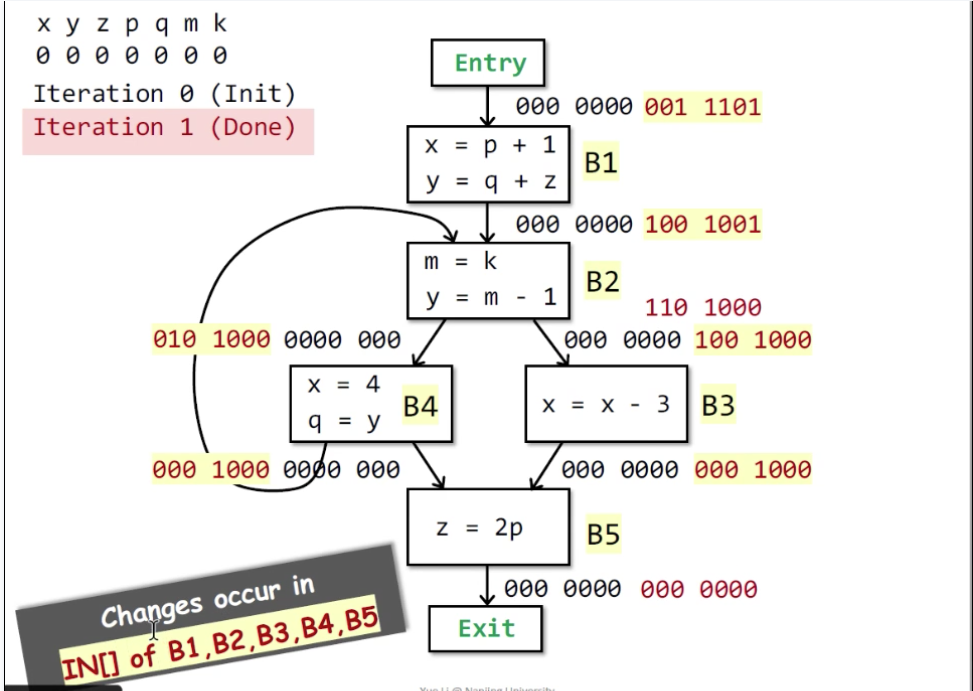
因为上一轮即初始化IN[]都为0,现在变了,依据算法进行第二轮迭代。
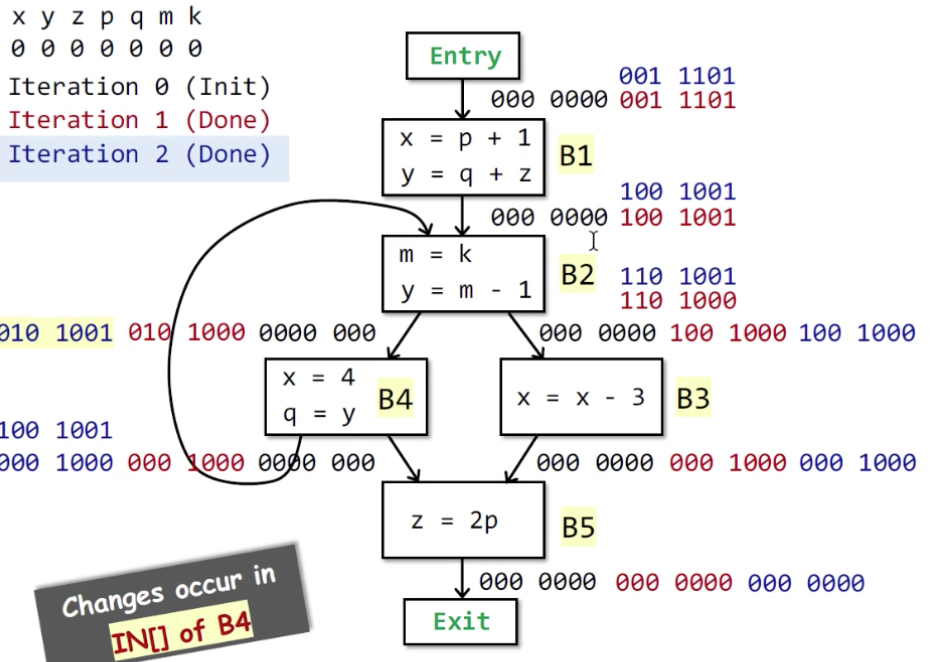
10.第二轮后IN[B4]变了,下一轮:
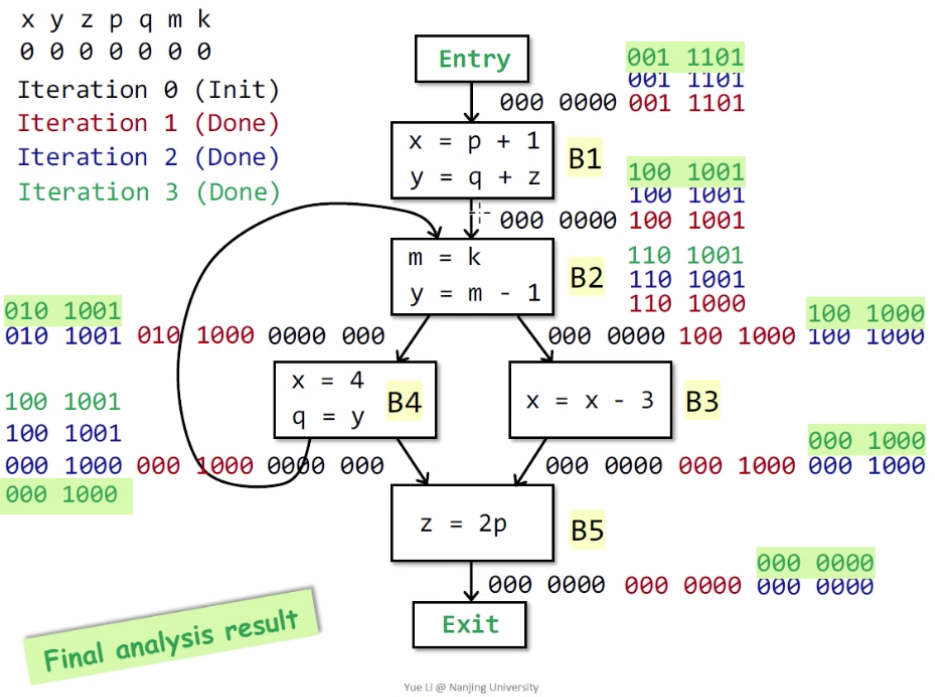
- 第三轮没有IN转变。