python层次聚类学习

Posted on

0x00 层次聚类描述

  1. 首把每一个样本点看作是一个cluster, 一开始有k个cluster
  2. 根据算法，聚合距离最近的两个cluster，形成k-1个cluster
  3. 循环直至一个最大的cluster形成
  4. 形成一张树状图区分不同的clusters

0x02 准备数据集

命名规则

  • X - 实验样本
  • n - 样本数量
  • m - 样本特征数量
  • Z - 集群关系数组
  • k - 集群数量

生成实验样本

矩阵X.shape == (n, m)，现在我有十个随机点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
import matplotlib.pyplot as plt

X = np.array([[5,3],
    [10,15],
    [15,12],
    [24,10],
    [30,30],
    [85,70],
    [71,80],
    [60,78],
    [70,55],
    [80,91],])

labels = range(1, 11)
plt.figure(figsize=(10, 7))
plt.subplots_adjust(bottom=0.1)
plt.scatter(X[: ,0], X[: ,1], label='True Position')

for label, x, y in zip(labels, X[:, 0], X[:, 1]):
    plt.annotate(
        label,
        xy=(x, y), xytext=(-3, 3),
        textcoords='offset points', ha='right', va='bottom')
plt.show()

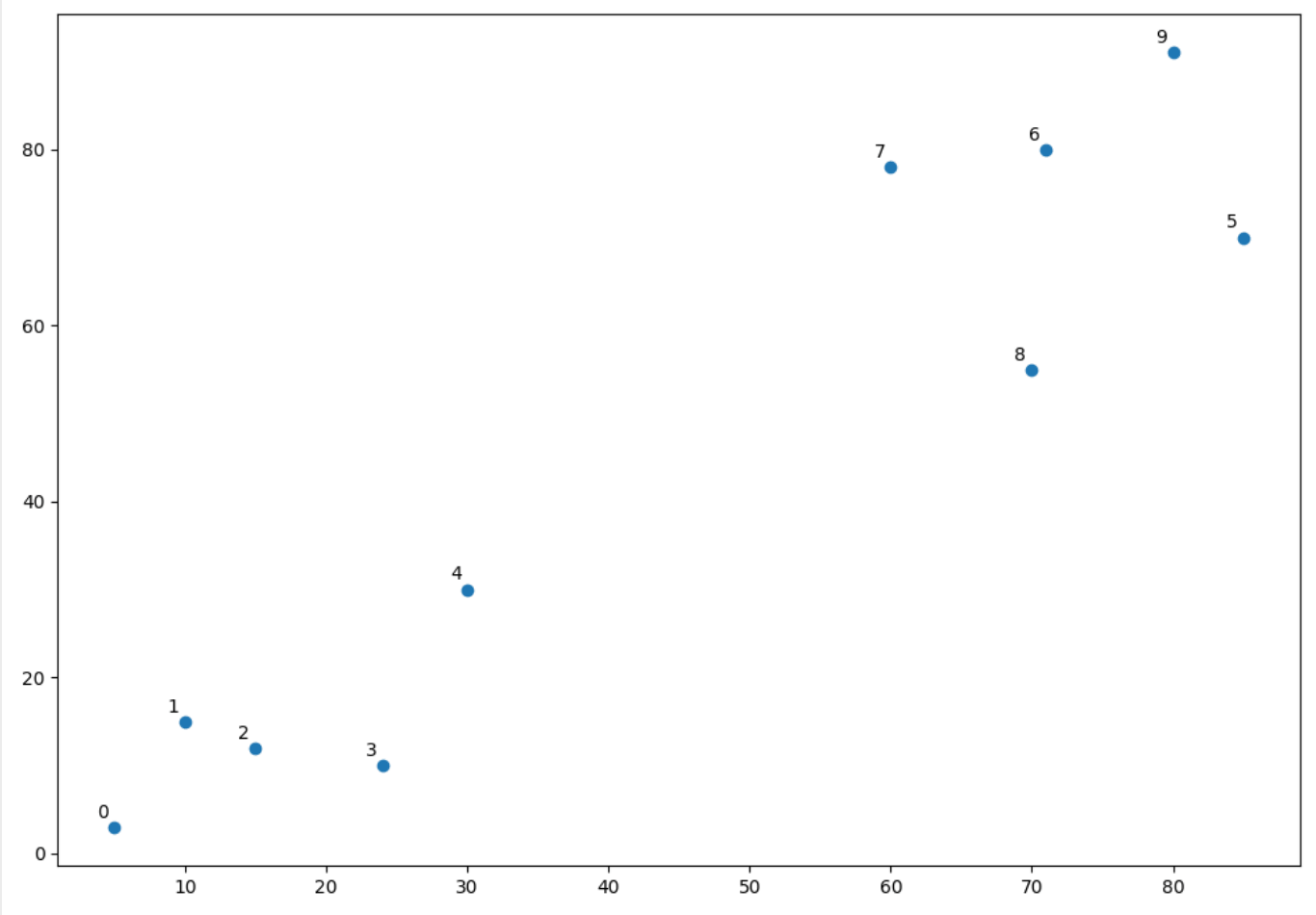
0x02 进行层次聚类

1
Z = linkage(X, method='ward') #average, single, complete...

method选择一个 距离算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage

X = np.array([[5,3],
    [10,15],
    [15,12],
    [24,10],
    [30,30],
    [85,70],
    [71,80],
    [60,78],
    [70,55],
    [80,91],])

Z = linkage(X, method='ward')
print(Z)

打印粗来：

1
2
3
4
5
6
7
8
9
[[  1.           2.           5.83095189   2.        ]
 [  6.           7.          11.18033989   2.        ]
 [  3.          10.          13.88044188   3.        ]
 [  0.          12.          17.98147195   4.        ]
 [  5.           8.          21.21320344   2.        ]
 [  9.          11.          21.73323108   3.        ]
 [  4.          13.          32.79634126   5.        ]
 [ 14.          15.          33.64322616   5.        ]
 [ 16.          17.         185.44001726  10.        ]]

每一行是[idx, idx2, dist, sample_count]可以看到是本来， 第一行就是对应层次聚类的第一步， 每一个点作为一个cluster, 其中1号点和2号点是聚类最近，为5.83...，于是这两个点在此步骤聚成了一个cluster, 有两个样本点。现在有k-1个cluster。然后第二步...。

看到第3步中，开始出现9号以外的点。此算法中，任何idx>=len(X)的下标指向Z[idx-len(X)]中建立的集群。

也就是说，10代表着第Z[10-10]也就是Z[0]第一步聚成的cluster与3进行合并。也就是X[[1,2,3]]

1
2
3
4
5
print X[[1,2,3]]
#=> output:
[[10 15]
 [15 12]
 [24 10]]

单看他们的坐标点应该是挺近，看图：

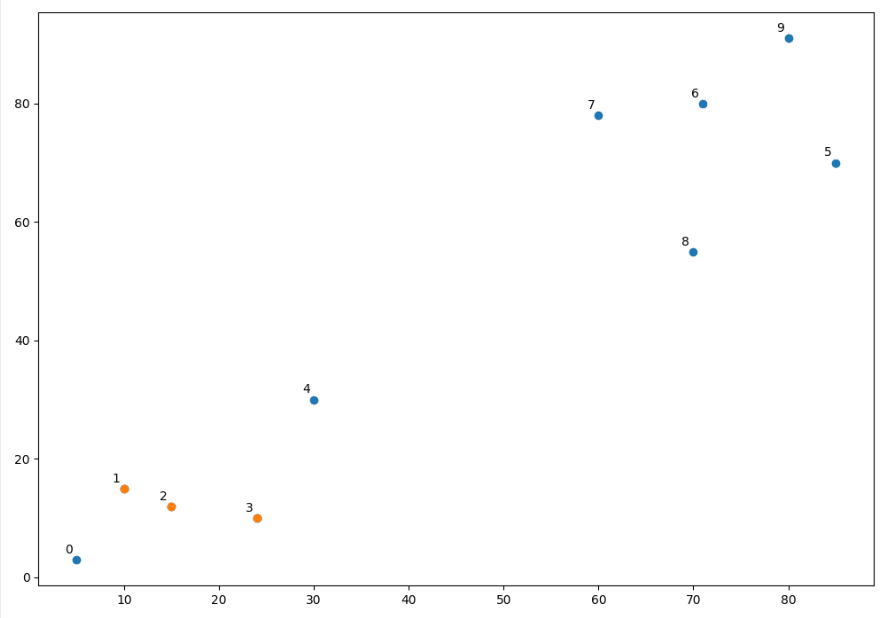
挺近...

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage

X = np.array([[5,3],
    [10,15],
    [15,12],
    [24,10],
    [30,30],
    [85,70],
    [71,80],
    [60,78],
    [70,55],
    [80,91],])

labels = range(0, 10)
idx = [1,2,3]
plt.figure(figsize=(10, 7))
plt.subplots_adjust(bottom=0.1)
plt.scatter(X[: ,0], X[: ,1], label='True Position')
plt.scatter(X[idx,0], X[idx,1], label='True Position')

for label, x, y in zip(labels, X[:, 0], X[:, 1]):
    plt.annotate(
        label,
        xy=(x, y), xytext=(-3, 3),
        textcoords='offset points', ha='right', va='bottom')
plt.show()

Z = linkage(X, method='ward')
print(X[[1,2,3]])

0x03 树状结构图（Dendrograms）

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage

X = np.array([[5,3],
    [10,15],
    [15,12],
    [24,10],
    [30,30],
    [85,70],
    [71,80],
    [60,78],
    [70,55],
    [80,91],])

linked = linkage(X, 'single')

labelList = range(0, 10)

plt.figure(figsize=(10, 7))
dendrogram(linked,
            orientation='top',
            labels=labelList,
            distance_sort='descending',
            show_leaf_counts=True)
plt.show()

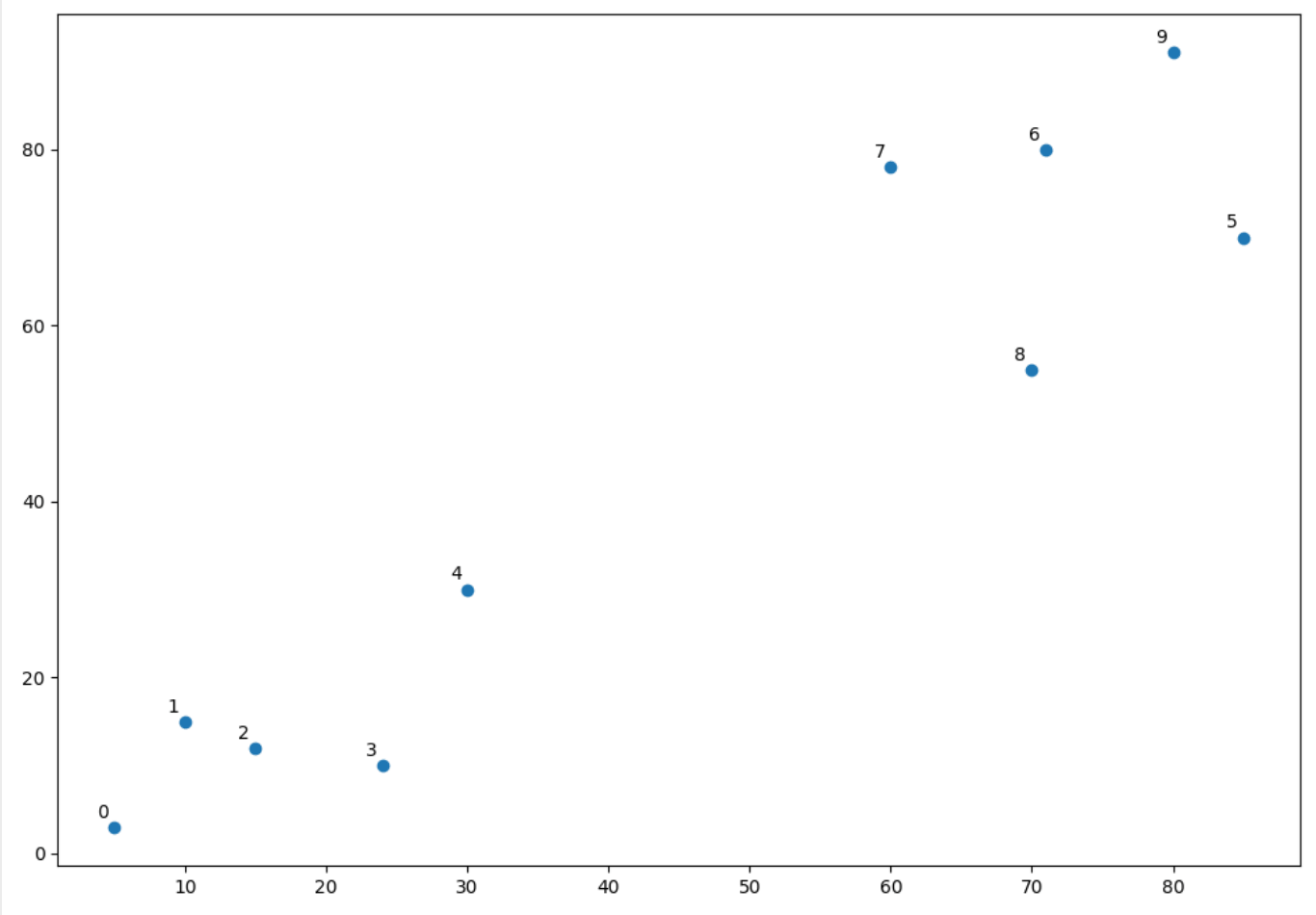
对就是这个图，让我们先，从下往上捋一捋。横坐标就是特征嘛，纵坐标看那个连接位置，就是他们聚在一起时候的值，这里好像根据的是欧几里得距离...再看我们聚类时的第一步:

1
[  1.           2.           5.83095189   2.        ]

所以说第1，2个点聚的最低，聚集起来的位置大概是5.8...。依次向上，最终聚成一个cluster。

参考

[1] 利用 SciPy 实现层次聚类

[2] Hierarchical Clustering with Python and Scikit-Learn